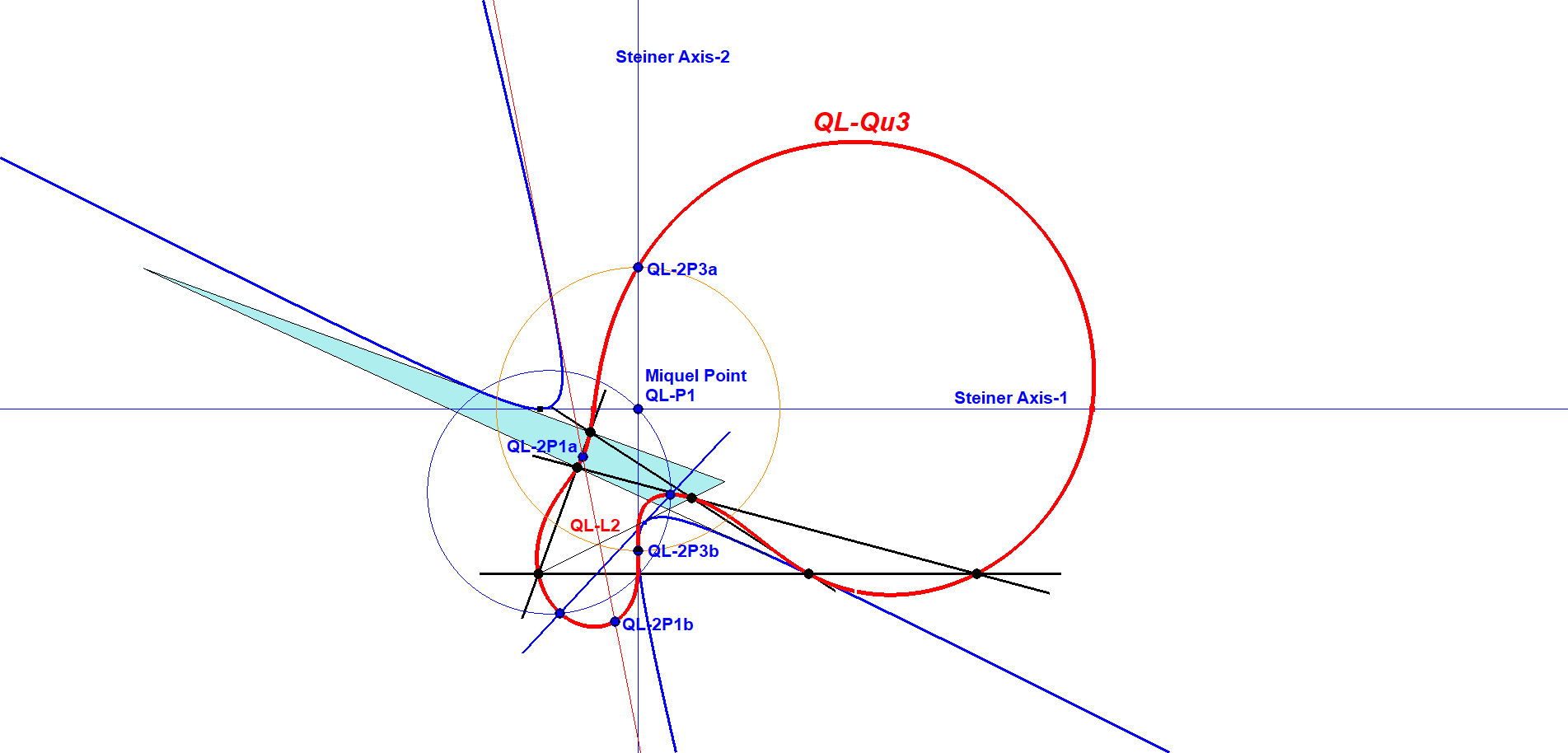
QL-Qu3: Schmidt Quartic
For a quadrilateral there are three pairs of intersections of opposite sides and for each pair a circle. The points, for which these circles are coaxal give a quartic. See QL-2P1 for a special case.
This quartic was found by Eckart Schmidt. See especially [34], QFG=message #364.
Let L1, L2, L3, L4 define a quadrilateral, then there are three pairs of intersections:
S12 = L1^L2, S34 = L3^L4 and S23 = L2^L3, S41 = L4^L1 and S13 = L1^L3, S24 = L2^L4.
We take for each pair the circumcircle through a point P and consider the locus of P for collinear centers of these three circles. This curve give a quartic.
Most information on this page comes from Eckart Schnidt. See for more details [34], QFG-messages #465, 490, 774, 1354, 1355, 1359, 1361, 1364, 1367, 1796, 3031, 3513, 3515.
There are also several properties related to QL-Qu3 considering the Quadrilateral formed by the sidelines of the QL-Diagonal Triangle QL-Tr1 and the Newton Line QL-L1. See [66], QPG-messages #173, #176-#181.
Construction
For the construction we need the 1st and 2nd Steiner axis (see QL-Tf1):
1. Construct an inscribed conic of the Diagonal Triangle QL-Tr1 with the 1st and 2nd Steiner axis (and Steiner Line QL-L2) as tangents.
2. The intersections of tangents at this conic and their image-circle wrt the Clawson-Schmidt Conjugate QLTf1 will give points of the quartic.
Equation in DT-coordinates
a2 b2 ( l2 – m2) z (l2 n2 x X + m2 n2 y Y – n4 z Z + 2 l2 m2 x y (x + y))
+ b2 c2 (m2 – n2) x (-l4 x X + l2 m2 y Y + l2 n2 z Z + 2 m2 n2 y z (y + z ))
+ a2 c2 (n2 – l2) y (l2 m2 x X – m4 y Y + m2 n2 z Z + 2 l2 n2 x z (x + z))
+ a4 (l2 – m2) (n2 – l2) y z (-m2 y (x + y) n2 z (x + z)
+ b4 (l2 – m2) (m2 – n2) x z (-n2 z (y + z) l2 x (x + y)
+ c4 (m2 – n2) (n2 – l2 x) y (-l2 x (x + z) m2 y (y + z) = 0
where X = 2 y z + x (x + y + z) ; Y = 2 x z + y ( x + y + z) ; Z = 2 x y + z (x + y + z);
Properties
- The quartic contains the six intersections of the quadrilateral.
- The quartic contains the Pluecker Points QL-2P1.
- The quartic contains the fixed points QL-2P3 of the Clawson-Schmidt Conjugate QL-Tf1.
- The quartic contains the vertices M1, M2 (unequal QL-P1) of the Miquel Triangles QA-Tr2 of the three quadrigon components.
- The quartic is invariant wrt the Clawson-Schmidt Conjugate QL-Tf1.
- The quartic is invariant wrt the three QA-Tf16 transformations for the three QG-versions of the reference quadrilateral.
Estimated human page views: 242
