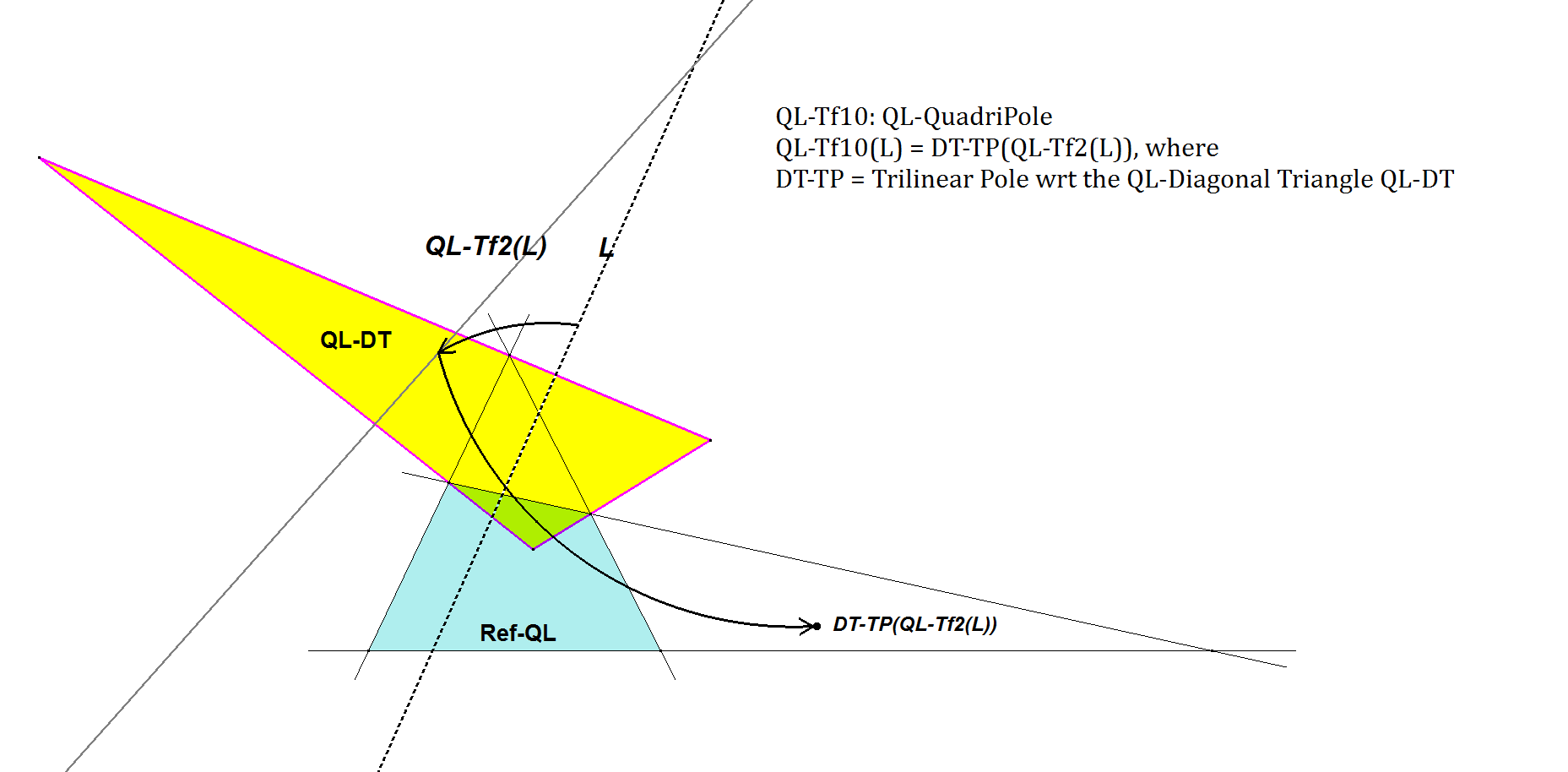
QL-Tf10: QL-QuadriPole
The QL-QuadriPole is an equivalent of the Tripole (also named Trilinear Polar) in a trilateral. It transforms in a Quadrilateral “harmonically” a line into a point.
QL-Tf10(L) = DT-TP(QL-Tf2(L)), where DT-TP = Trilinear Pole wrt the QL-Diagonal Triangle QL-DT (=QL-Tr1).
The combination QL-Tf10/QL-Tf11 in a Quadrilateral is the equivalent of the combination QA-Tf10/QA-Tf11 in a Quadrangle.
In particular QL-Tf10 is the dual of QA-Tf11 and has the same coordinates as QA-Tf11 when substituting (p:q:r) >(l:m:n).
QL-Tf10(L) = DT-TP(QL-Tf2(L)), where DT-TP = Trilinear Pole wrt the QL-Diagonal Triangle QL-DT (=QL-Tr1).
The combination QL-Tf10/QL-Tf11 in a Quadrilateral is the equivalent of the combination QA-Tf10/QA-Tf11 in a Quadrangle.
In particular QL-Tf10 is the dual of QA-Tf11 and has the same coordinates as QA-Tf11 when substituting (p:q:r) >(l:m:n).
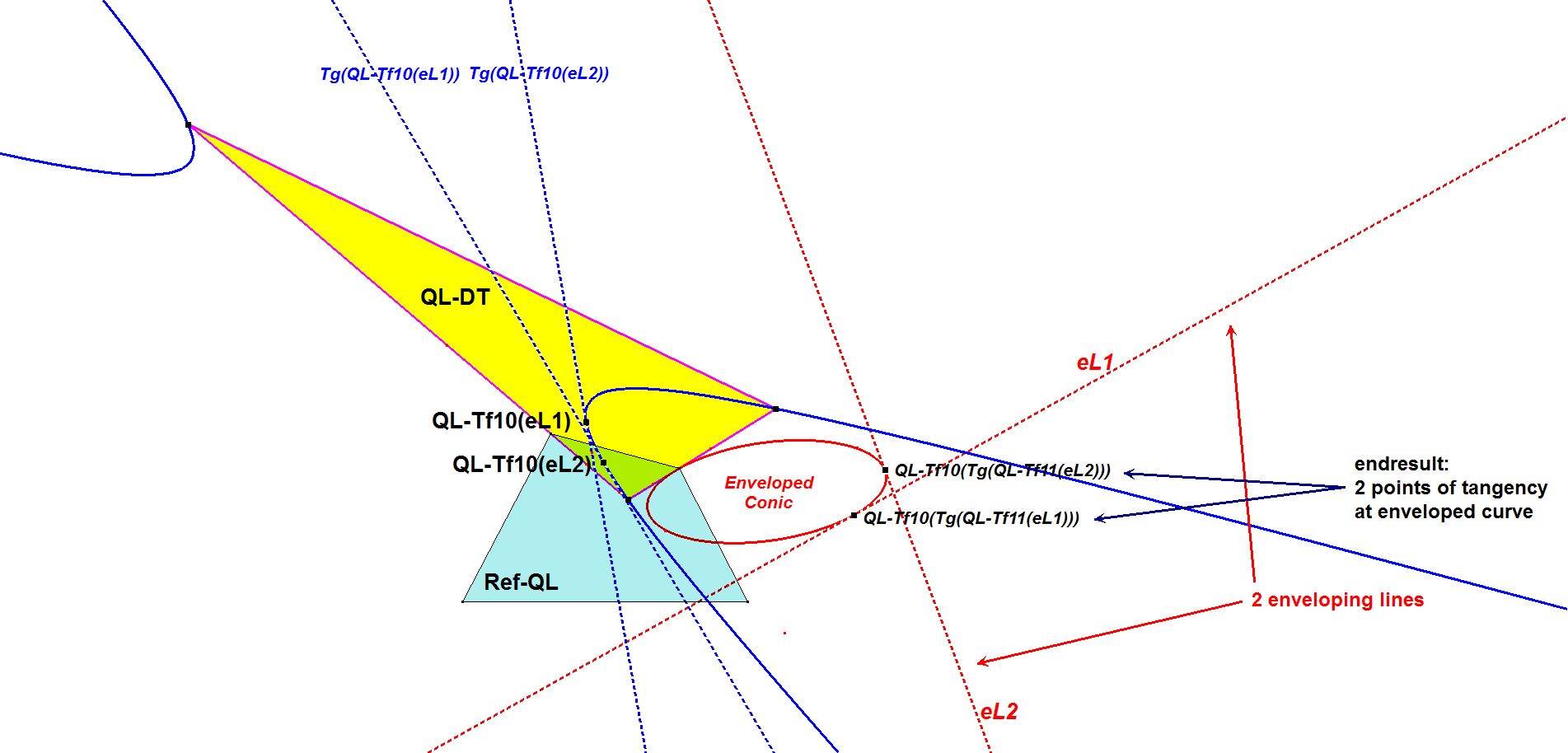
One of the advantages of QL-Tf10 is that enveloping lines eLi can be transformed by QL-Tf10 into points ePi, producing a point driven locus, whereafter the tangents at ePi can be obtained, which can be transferred back by QL-Tf10, delivering the points of tangency at eLi, which produce a point driven locus tangent to the initial enveloping lines. So an envelope of lines can be transferred into a point driven locus. See picture below and QL-8.
(m n (3 m n x - l n y - l m z) : l n (-m n x + 3 l n y - l m z) : l m (-m n x - l n y + 3 l m z))
(x/l2 : y/m2 : z/n2)
Properties
• QL-Tf10(QL-Tf11(P)) = P and QL-Tf11(QL-Tf10(L)) = L.
• QL-Tf10(L) also can be obtained as QA-Tf2*(DT-TP(L)), where QA-Tf2* = QA-Tf2-transformation wrt the dual QA with vertices Pi=DT-TP(Li) (i=1,2,3,4). Therefore it is also QA-Tf10(L) wrt the dual QA. See QL-8.
• QL-Tf10(QL-Tf11(P)) = P and QL-Tf11(QL-Tf10(L)) = L.
• QL-Tf10(L) also can be obtained as QA-Tf2*(DT-TP(L)), where QA-Tf2* = QA-Tf2-transformation wrt the dual QA with vertices Pi=DT-TP(Li) (i=1,2,3,4). Therefore it is also QA-Tf10(L) wrt the dual QA. See QL-8.