QL-Tf11: QL-QuadriPolar
The QL-QuadriPolar is an equivalent of the Tripolar (also named Trilinear Polar) in a trilateral. It transforms in a Quadrilateral “harmonically” a point into a line.
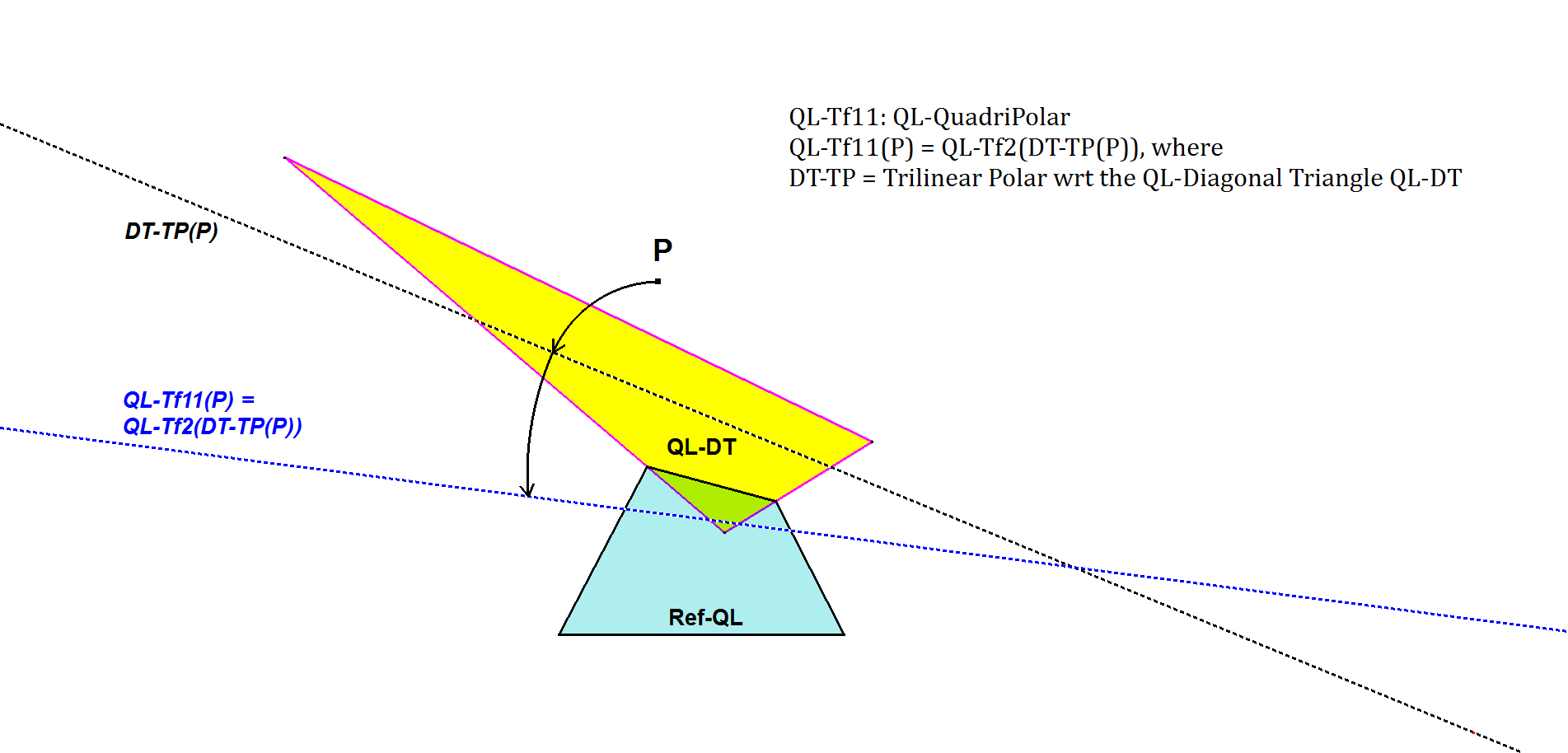
QL-Tf11(P) = QL-Tf2(DT-TP(P)), where DT-TP = Trilinear Polar wrt the QL-Diagonal Triangle QL-DT (=QL-Tr1).
The combination QL-Tf10/QL-Tf11 in a Quadrilateral is the equivalent of the combination QA-Tf10/QA-Tf11 in a Quadrangle.
In particular QL-Tf11 is the dual of QA-Tf10 and has the same coordinates as QA-Tf10 when substituting (p:q:r) >(l:m:n).
QL-Tf11 is used by the 1st construction of the Involutary Centerline QL-Tf8.
CT-coordinates
Let P = (x:y:z), then QL-Tf11(P) =
(l (2 l x + m y + n z) : m (l x + 2 m y + n z) : n (l x + m y + 2 n z))
DT-coordinates
Let P = (x:y:z), then QL-Tf11(P) =
(l2 x : m2 y : n2 z)
Properties
- QL-Tf11(QL-Tf10(L)) = L and QL-Tf10(QL-Tf11(P)) = P.
- QL-Tf11(P) also can be obtained as DT-TP(QA-Tf2*(P)), where QA-Tf2* = QA-Tf2-transformation wrt the dual QA with vertices Pi=DT-TP(Li) (i=1,2,3,4). Therefore it is also QA-Tf11(P) wrt the dual QA. See QL-8.
Estimated human page views: 477
