QL-Tf6: QL-Trilinear Polar
QL-Tf6 is a transformation mapping a point into a line.
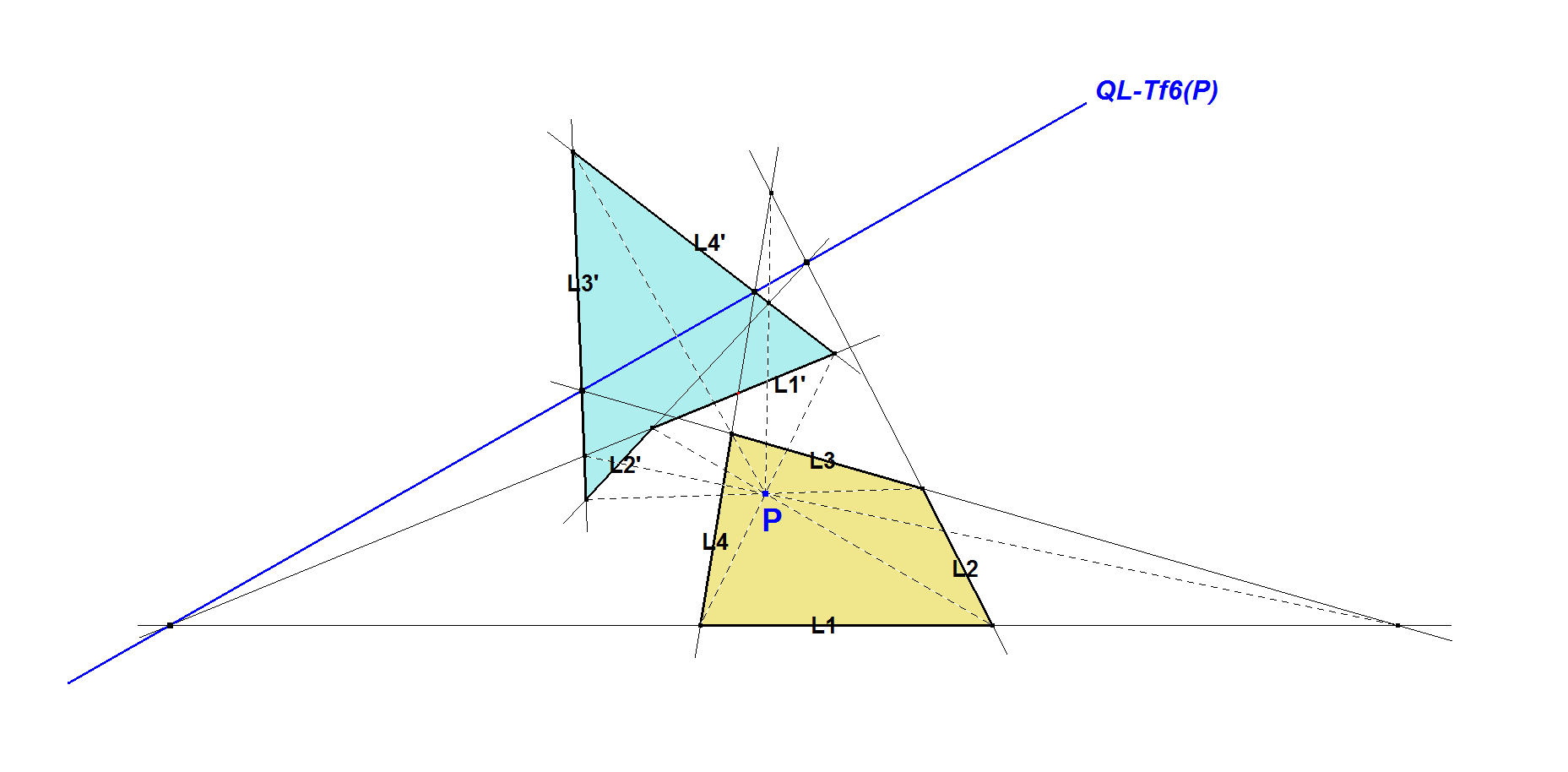
Let L1.L2.L3.L4 be a quadrilateral. Let P be a random point. Let L1’ be the trilinear polar of P wrt triangle L2.L3.L4.
Similarly, we have L2’, L3’, L4’. Then quadrilaterals L1.L2.L3.L4 and L1’.L2’.L3’.L4’ are point perspective (meaning that lines through Li^Lj and Li’^Lj’ are concurrent (i,j elements from (1,2,3,4)) and line perspective (meaning that Li^Li’ are collinear (i=1,2,3,4)). Last item being the line through L1^L1’, L2^L2’, L3^L3’ and L4^L4’ is called the QL-Trilinear Polar.
This transformation was mentioned as dual transformation of QA-Tf7 by Tsihong Lau in [34], QFG#2154. See also QFG#2161.
This transformation was also mentioned as the collinear line of the 3 versions of QA-Tf2(P) (see QL-3QG1) by Eckart Schmidt in [34], QFG#2176, #2177.
The equivalent of this transformation in a quadrangle is QA-Tf7.
QA-Tf7 and QL-Tf6 have corresponding coordinates (interchange (p:q:r) with (l:m:n)).
Inverse Transformation QL-Tf6R
Note that P is perspector and L is Perspectrix of perspective quadrangles L1.L2.L3.L4 and L1’.L2’.L3’.L4’. QL-Tf6 maps the Perspector P into the Perspectrix L.
There is an inverse Transformation QL-Tf6R that will map Perspectrix L into three point images P1,P2,P3, being the 3 possible related Perspectors.
For these points QL-Tf6(Pi) = L. They are the common intersections of the 3 versions of the conics QA-Tf2(L) and lie on a QL-Tr1-Circumconic.
When L = QL-L1, then the three points Pi are the 3 common intersections (unequal QL-P24) of the QL-Tr1-Circumconic through QL-P8 and QL-P13 and a circle round the reflection of QL-P9 in QL-P6 through QL-P24. See [34], Eckart Schmidt, QFG#2176, #2177.
CT-coordinates
Given point P(x:y:z), then coordinates QL-Tf6(P) are:
(y z (2 l x + m y + n z) : x z (l x + 2 m y + n z) : x y (l x + m y + 2 n z))
Properties
- The QL-Trilinear Polar of QL-P1 is QL-L11.
- The QL-Trilinear Polar of QL-P8 is a line through QL-P23 and is the 2nd asymptote of QL-Co2 and is parallel to the QL-Trilinear Polar of QL-P23.
- QL-Tf6(QL-P8) // QL-Tf6(QL-P23) // QL-Tf2(QL-Tf6(QL-P8)) // QL-Tf6(QL-L9 ^ QL-P8.QL-P13)). See [34], Eckart Schmidt, QFG#2176, #2177.
- The QL-Trilinear Polar of QL-P13 is a line through QL-P19 parallel to QL-L9.
- QL-Tf6 maps the vertices of QL-Tr1 into the opposite lines of QL-Tr1. See [34], Eckart Schmidt, QFG#2176, #2177.
- QL-Tf6 maps the vertices of QL-Tr2 into the line at infinity. See [34], Eckart Schmidt, QFG#2176, #2177.
- QL-Tf6(P) is the collinear line of the 3 QL-versions of QA-Tf2(P). See [34], Eckart Schmidt, QFG#2176, #2177, #3022.
Estimated human page views: 429
