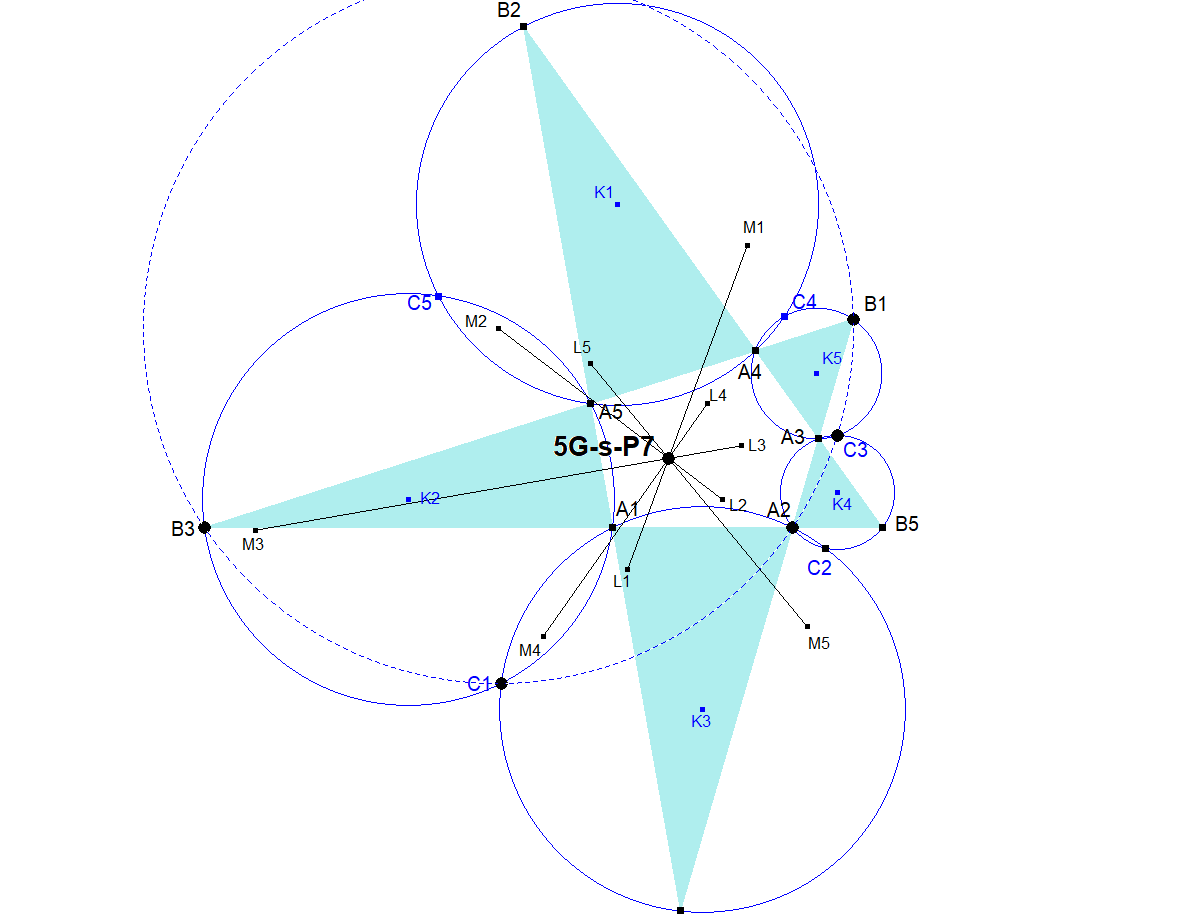
5G-s-P7 3rd 5G-Hung’s Point
Let Ai, i = 1, 2, . . . , 5, be any five points.
Taking subscripts modulo 5, we denote, for i = 1, 2, . . . , 5,
the intersection of the lines AiAi+1 and Ai+2Ai+3 by Bi+4,
the second intersection of two circles (AiAi+1Bi+3) and (Ai+1Ai+2Bi+4) by Ci+1
and the center of circle (AiCi+1Ai+2) by Li+1.
Follow Miquel’s theorem then five points Bi-1, Ci-1, Ai, Ci+1, and Bi+1 lies on a circle (Mi) with taking subscripts modulo 5.
Then five lines LiMi, for i = 1, 2, . . . , 5, are concurrent at a point 5G-s-P7.
This theorem was found by Tran Quang Hung at [70], Theorem 5.
Estimated human page views: 243
