QA-P4: Isogonal Center
This point is mentioned by H. M. Cundy and C. F. Parry [18] as „Isoptic (or Bennett) point”. As shown in the picture below, it is the Inverse of the Isogonal Conjugate of Pi wrt (circumcircle) PjPkPl. Many properties of this point are listed by Stärk [16] under the name “Tangentialpunkt” wrt the QA-DT-P4 Cubic (QA-Cu1). Other properties also can be found in [15f].
In the discussion of Hyacinthos messages (See [11] #19635, #19649) the point is seen as Homothetic Center. It is called the Isogonal Center because it can be constructed as Homothetic Center of the Reference Quadrangle with the 2nd Isogonal Conjugate Quadrangle and because it has an isogonal conjugate relationship with basic points QA-P2 and QA-P3 (see properties below).
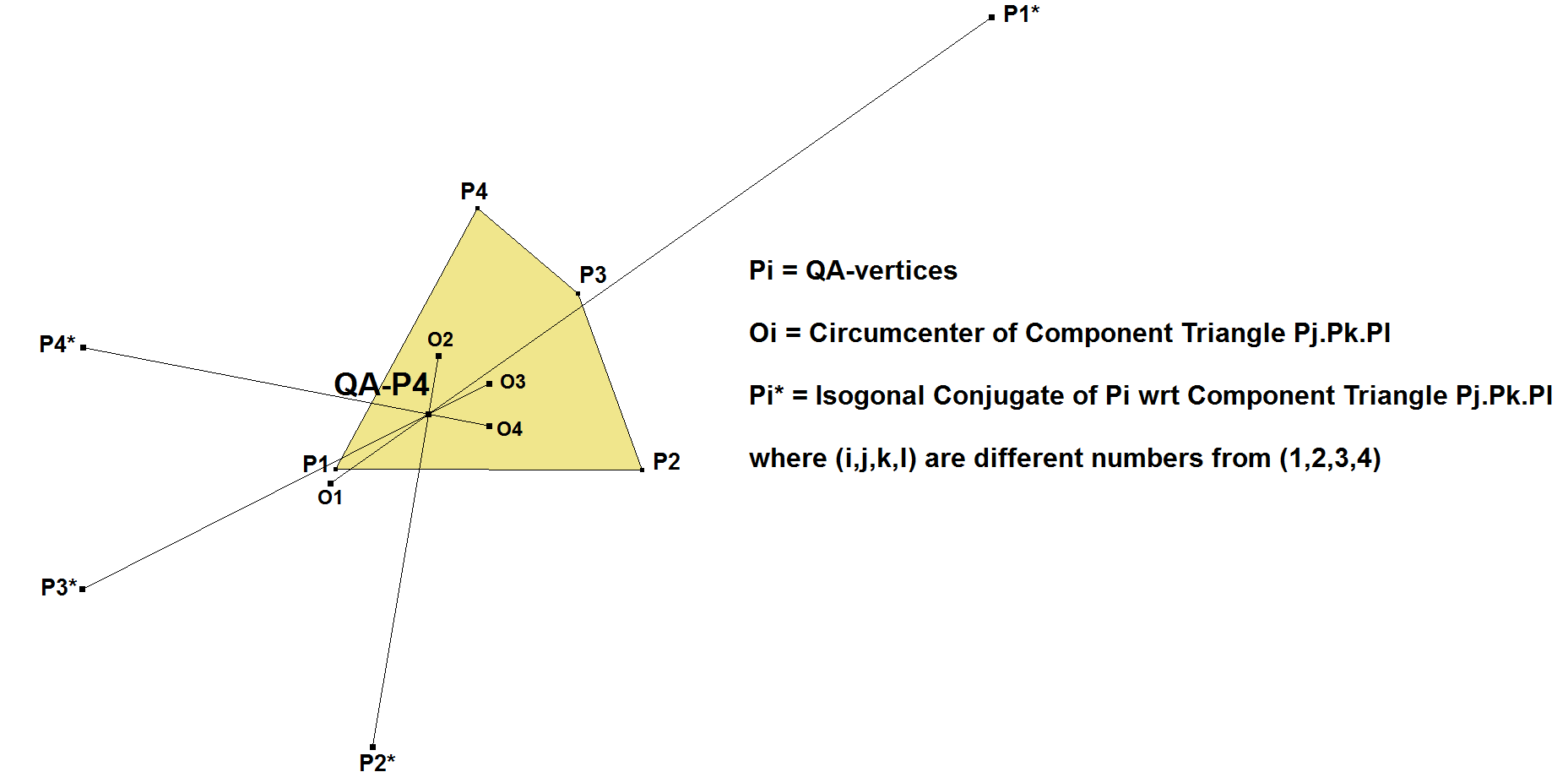
Construction
It can be constructed as the common point of the lines Oi.Qi, where Oi is the Circumcenter of Pj.Pk.Pl and Qi is the Isogonal Conjugate of Pi wrt Pj.Pk.Pl.
QA-P4 has equivalent functions as the Circumcenter in a Cyclic Quadrangle:
1st CT-Coordinate
a2 (a2 qr/p + b2 r + c2 q – 2 SA (p+q+r))
1st DT-Coordinate
b2 c2 p4 – a4 q2 r2 + (b2 – c2) p2 (-c2 q2 + b2 r2)
Properties
- QA-P4 lies on these lines:
- QA-P4 = Homothetic Center of the 2nd Circumcenter Quadrangle. See [23].
- QA-P4 = Homothetic Center of the 2nd Perpendicular Bisector Quadrangle. See[9].
- QA-P4 = Homothetic Center of the 2nd Isogonal Conjugate Quadrangle
- QA-P4 = Homothetic Center of the 1st Circumcenter Quadrangle and the 1st Isogonal Conjugate Quadrangle. See [11] #19635.
- QA-P4 = Inverse of Isogonal Conjugate of Pi wrt (circumcircle) Pj.Pk.Pl. See [18].
- QA-P4 = Isogonal Conjugate of the Reflection of Pi in QA-P2 wrt Pj.Pk.Pl. See [18].
- QA-P4 = Isogonal Conjugate of QA-P3 wrt the Miquel Triangle QA-Tr2. See [15c] page 5.
- QA-P4 = Anticomplement of the Isogonal Conjugate of QA-P3 wrt the QA-Diagonal Triangle QA-Tr1. See [15f] theorem (25).
- QA-P4 = Involutary Conjugate (QA-Tf2) of QA-P41.
- QA-P4 lies on the 5th Point tangent (see QA-Tf9) at QA-P3.
- QA-P4 lies on the circumcircle of the triangle formed by the 3 QA-versions of QG-P19.
- QA-P4 is also the second intersection point of the circles through the Miquel Point (QL-P1) and 2 opposite vertices of a QA-Quadrigon.
- QA-P4 lies on the QA-DT-P4 Cubic (QA-Cu1).
- Let M = Diagonal Point Pi.Pj ^ Pk.Pl. Now M.QA-P4 and M.QA-P2 are symmetric wrt the angle bisector of lines Pi.Pj and Pk.Pl for all combinations of (i,j,k,l) (1,2,3,4). See [16] page 8.
- Let ABCD be a Quadrangle. The 4 circles ABC, ABD, BCD, CAD can be seen from QA-P4 under the same angle. That’s why this point is also called the Isoptic Point. This feature is especially the case when 1 of the 4 points lies within the triangle of the other 3 points (see [16] and [22]).
- The Isogonal Center of the Quadrangle S1.S2.S3.QA-P4 is the Involutary Conjugate (QA-Tf2) of QA-P4 (note Eckart Schmidt).
- At Quadrigon-level QA-P4 is the Clawson-Schmidt Conjugate of the Diagonal Crosspoint (QG-P1). See [15f] theorem (28).
- At Quadrigon-level the Pedal Quadrangle of QA-P4 is a parallelogram with center QA-P6 (Parabola Axes Crosspoint). See [15 f] theorem (23). This parallelogram has the property that its angles are equal to those formed by the diagonals of the Reference Quadrangle (just like Varignon’s Parallelogram). It also coincides with Varignon’s Parallelogram if and only if the Reference Quadrangle is cyclic. See [27].
- QA-P4 lies on all 6 circles of similitude of the circumscribed circles of the component triangles of a quadrangle.
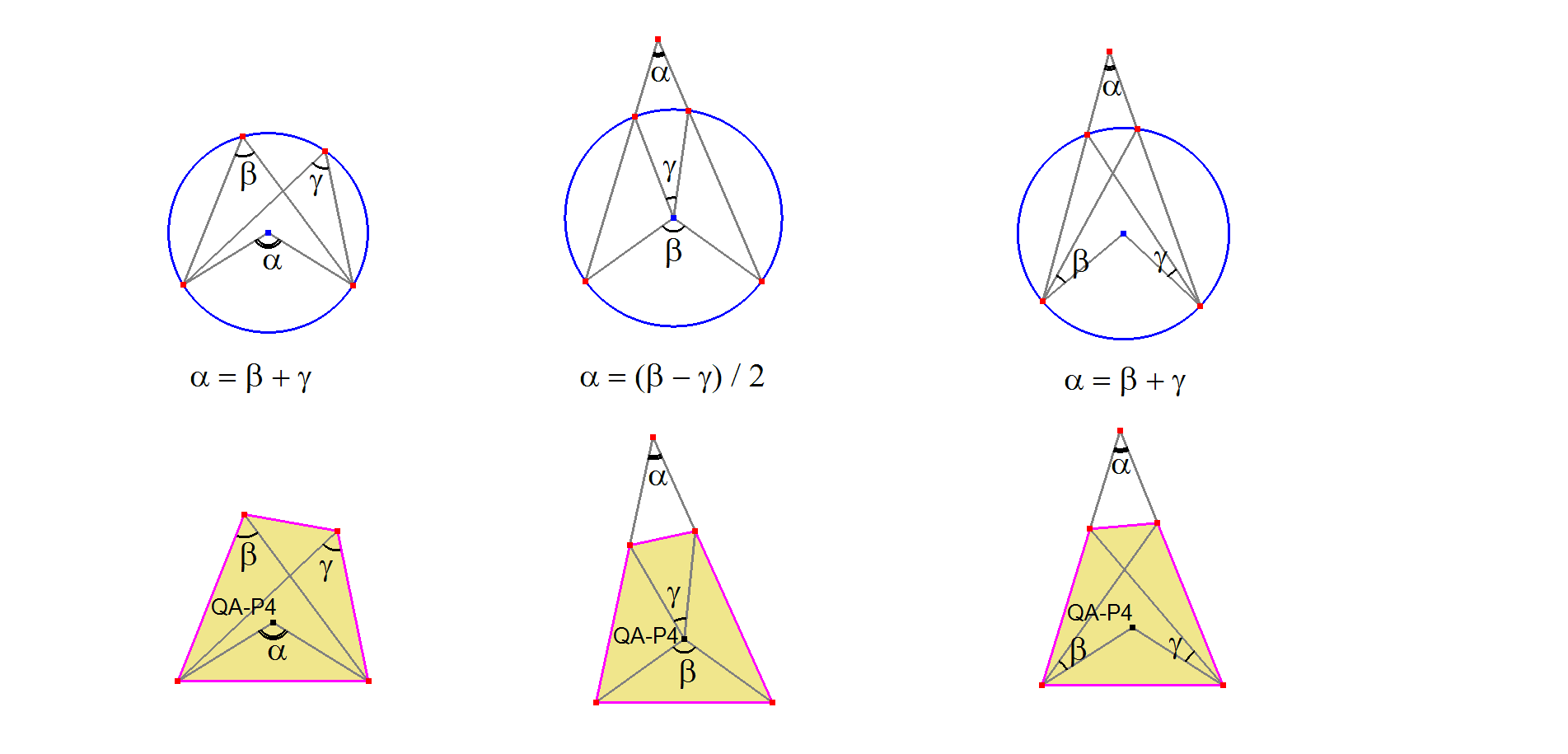
- The (directed) angle subtended by any of the quadrangles sides at QA-P4 equals to the sum of the angles subtended by the same side at the two remaining vertices. See [11], message # 19640 and [27].
- The distance from QA-P4 to any vertex is inversely proportional to the radius of the circumscribed circle of the component triangle determined by the remaining three vertices. See [27].
- The powers of QA-P4 with respect to circumscribed circles of the component triangles are proportional to the squares of the radii of the circumscribed circles of the component triangles. See [27].
- QA-P4 is the point at infinity if and only if the vertices of the quadrangle form an orthocentric system. See [27].
- In a Quadrigon the Triangle formed by QA-P4 and the vertices of the QA-Diagonal Triangle (QA-Tr1) unequal QG-P1 is perspective with the QA-Miquel Triangle (QA-Tr2) with perspector QG-P16 (Eckart Schmidt, November 26, 2012).
- QA-P4 is concyclic in a Quadrigon with QG-2P2a, QG-2P2b, QG-P19. The circle through these points is a QL-Tf1 image of QA-Ci1 (Eckart Schmidt, December 12, 2012).
- Let Hi be the Orthocenter of Component Triangle Pj.Pk.Pl. Let line Li be the isogonal conjugate wrt Pj.Pk.Pl of the conic (Hi,P1,P2,P3,P4). QA-P4 is the point of concurrency of L1, L2, L3, L4 (Seiichi Kirikami, July 14, 2013). See [34], Quadri-Figures-Group, messages 117&118.
- Let P1.P2.P3.P4 be the Reference Quadrangle. Let O1 be the circumcenter of Component Triangle P2.P3.P4. The reflections of O1.QA-P4 in the sidelines of P2.P3.P4 bound a triangle that is perspective with P2.P3.P4 with perspector J1. This point is lying on the circumcircle of P2.P3.P4 and moreover is incenter or excenter of P2.P3.P4. Similarly J2, J3, J4 are constructed. P1.P2.P3.P4 and J1.J2.J3.J4 are perspective. Their perspector is QA-P3. See [34], QFG messages #609, #624, #625, #627.
- The QL-Clawson-Schmidt Conjugate (QL-Tf1) of QA-P4 is QG-P1.
- The QA-Orthopole (QA-Tf3) of QA-P4 is QA-P2.
- Let Nij be the feet of the perpendiculars from QA-P4 to Pi.Pj.. Then the 4 versions of circles through Nij, Nik, Nil (for all combinations (i,j,k,l) (1,2,3,4)) have one common point, which is QA-P4 (Seiichi Kirikami, July 17, 2013). See [34] Quadri-Figures-Group, message # 126.
- QA-P4 is the Center of the QA-Möbius Conjugate because of many special properties. See QA-Tf4.
- In a cyclic Quadrangle QA-P4 is the midpoint of Pi and the AntiComplement of QA-P2 wrt Triangle Pj.Pk.Pl. See [34], QFG#972.
- QA-P4 is the Perspector of the QG-P16 Triple Triangle and the QL-P1 Triple Triangle (see QA-Tr-1).
- A QA-circumconic through QA-P4 contacts QA-Cu1 in this point. See [34], Eckart Schmidt, QFG-message #1666.
Estimated human page views: 1583
