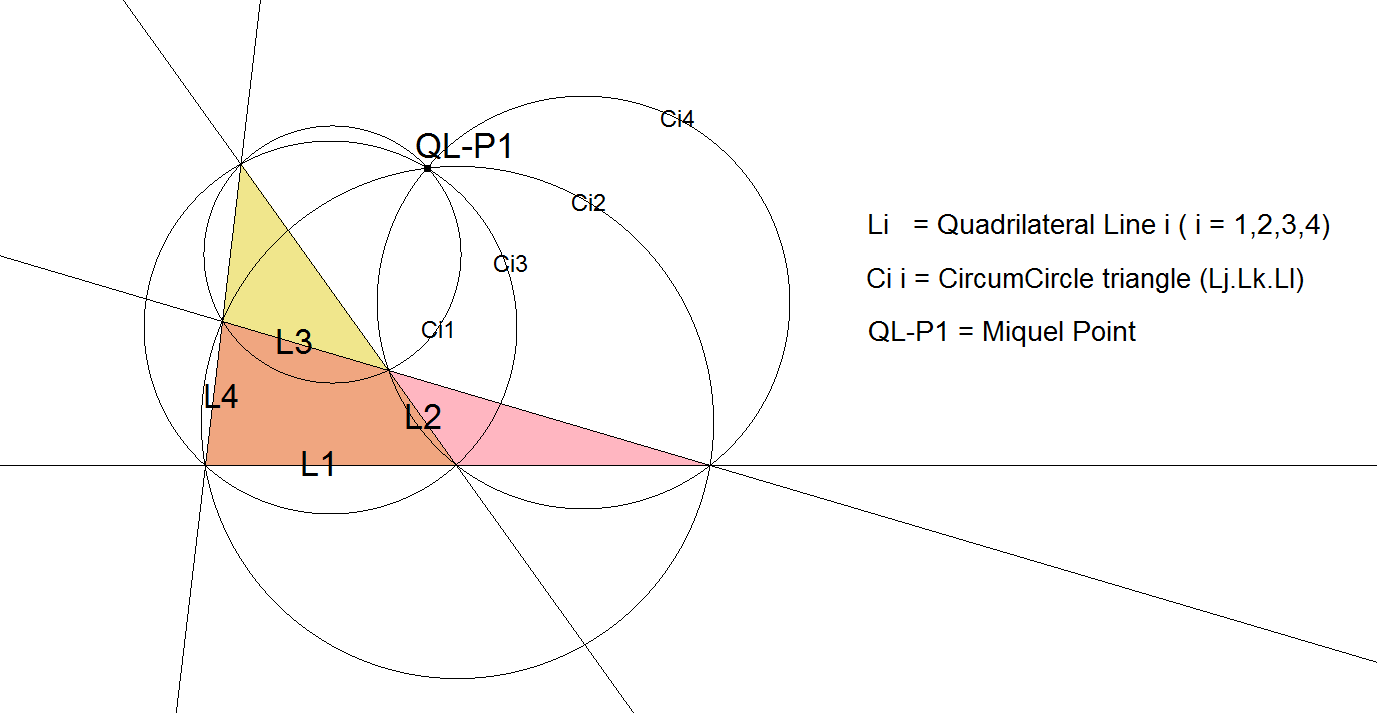
QL-P1: Miquel Point

The Miquel Point is the common point of the circumcircles of the 4 component triangles of the Reference Quadrilateral.

This point is also called the Steiner Point or Clifford Point.

This point is also called the focal point by J.W. Clawson. See [22] page 250 and [31].

He describes 134 circles of “more or less interest” through this point.

1^st CT-coordinate

a² m n/(m – n)

1^st DT-coordinate

b²/(l²-n²) – c²/(l²-m²)

Properties

• The Miquel Point QL-P1 lies on these lines:
  • QL-P7.QL-P19 = QL-L5    (2 : -1 => QL-P1 = Reflection of QL-P7 in QL-P19)
  • QL-P8.QL-P24
  • QL-P10.QL-P16                 ( 1 : 1 => QL-P1 = Midpoint of QL-P7 and QL-P19)
  • QL-P20.QL-P21                 (-1 : 2=> QL-P1 = Reflection of QL-P21 in QL-P20)
  • QA-P4.QG-P16
  • QA-P3.QG-P1

• Note: The collinearity of QG-P1, QA-P3 and QL-P1 is discussed at [34], QFG-messages #2987, #2989, #2990, #2992, #3000, #3009, #3011, #3027, #3029 and proven synthetically at [60], page 150 (O ~ QA-P3, R ~ QG-P1, Mr ~ QL-P1).

• QL-P1 is the Railway Watcher (see QL-L-1) of:
  • QL-L2 and QL-L3,
  • QL-L1 and the asymptote of QL-Cu1.
• QL-P1 is the focus of the unique inscribed parabola of the Reference Quadrilateral (see [4] page 49).
• QL-P1 and the circumcenters of the 4 component triangles of the Reference Quadrilateral are concyclic on QL-Ci3 (Miquel Circle).
• QL-P1 lies on the 3 coaxal circles:
  • QL-Ci3 (Miquel Circle),
  • QL-Ci5 (Plücker Circle),
  • QL-Ci6 (Dimidium Circle).
• QL-P1 lies on the Circle defined by the 3 QL-versions of QA-P9, being QL-Ci3 (note Eckart Schmidt).
• QL-P1 lies on QL-Ci2 (Nine-point Circle of the QL-Diagonal Triangle). See [32] as well as [11], Hyacinthos message # 12896 from Quang Tuan Bui.
• QL-P1 lies on QL-Cu1 (QL-Quasi Isogonal Cubic).
• QL-P1 lies on QL-Qu1 (Morley’s QL-Mono Cardioide).
• QL-P1 is the isogonal conjugate of the Infinity Point of the Newton line with respect to each of the four component triangles (see [4] page 41).
• The symmetric lines of the Steiner Line QL-L2 in the 4 quadrilateral lines coincide at QL-P1.
• QL-P1 relates pairwise to all present line segments in the quadrilateral. It is the center of similarity of line segments Li^Lk . Li^Ll and Lj^Lk . Lj^Ll, where (i,j,k,l) ∊ (1,2,3,4). As a consequence triangles QL-P1 . Li^Lk . Li^Ll and QL-P1 . Lj^Lk . Lj^Ll are similar (see also [9]).
• QL-P1 is the perspector of the QL-Diagonal Triangle and the Triangle formed by the 3 QL-versions of QA-P3 (Gergonne-Steiner Point).
• The Clawson-Schmidt Conjugate (QL-Tf1) is “centered” around QL-P1.
  • Lines through QL-P1 are transformed in other lines through QL-P1.
  • Lines not through QL-P1 are transformed in a circle through QL-P1.
  • Circles with circumcenter QL-P1 are transformed in another circle with circumcenter QL-P1.
• The Miquel Point QL-P1 of a Quadrilateral L1.L2.L3.L4 is the Isogonal Conjugate of the Infinity Point of the Trilinear polar of the Isotomic Conjugate of the Trilinear Pole of Li wrt Triangle Lj.Lk.Ll, where (i,j,k,l) is any combination of {1,2,3,4}.
• In short: MP = Ic(Ip(TPolar(It(TPole(Li))))).
• (Francisco Javier García Capitán, Hyacinthos message #21271 [11], Nov. 5, 2012)
• QL-P1 is the QA-Tf2 image (Involutary Conjugate) of QG-P16 (Eckart Schmidt, November 26, 2012).
• QL-P1 lies on the Polars (see [13], Polar) of QL-P2, QL-P7, QL-P9 wrt QL-Co1.
• Let ABCD be a Component Quadrigon of the Reference Quadrilateral and let P be its Miquel Point. If m is the distance between the midpoints of the diagonals of ABCD, then PA/(AB*AD) = PB/(BA*BC)=PC/(CB*CD)=PD/(DA*DC)=1/(2*m) (see [11], Hyacinthos message # 9086).
• Let Ti = Triangle formed by the 3 lines Lij, Lik, Lil ((i,j,k,l) ∈ (1,2,3,4)) where Lmn = Line perpendicular to Ln at intersection point Lm^Ln.
• The 4 triangles Ti (i=1,2,3,4) have one common point, being QL-P1.
• Moreover the circumcenters of the 4 triangles Ti (i=1,2,3,4) lie on QL-Ci3.
• Found by Antreas P. Hatzipolakis, see [33], Anopolis messages # 466,467.
• The QA-Orthopole (QA-Tf3) of QL-P1 is a point on the Newton Line QL-L1.
• The QA-Möbius Conjugate (QA-Tf4) of QL-P1 is QG-P5.
• QL-P1 lies on the polar of QG-P16 wrt QG-Co2 (and invers) (Eckart Schmidt, October 9, 2013). See [34], QFG # 286.
• The QA-Triple Triangle of QL-P1 is Perspective and Cyclologic wrt all QA-Component Triangles ( [34], QFG#977 by Seiichi Kirikami). See QA-Tr-1.
• The QA-Triple Triangle of QL-P1 is Orthologic wrt the Triple Triangles of QG-P7, QG-P9 and QL-P6. See QA-Tr-1.
• The reflections of QL-P1 in the 4 basic lines of the Reference Quadrilateral lie on QL-L2. See [34], Seiichi Kirikami, QFG message # 1091.
• The reflections of QL-L2 in the 4 basic lines of the Reference Quadrilateral concur in QL-P1. See [34], Seiichi Kirikami, QFG message # 1095.
• The line through the intersection point of Li and Lj (i,j=1,2,3,4) and through the intersection point of the reflected lines of QL-L3 in Li and Lj passes through QL-P1. See [34], Seiichi Kirikami, QFG message # 1096.
• The Orthopole of ANY line through QL-P1 wrt ANY Component Triangle of the Reference Quadrilateral lies on QL-L3. See [33], Anopolis # 637.

Estimated human page views: 1032