5P-s-P1: 5P-Circumscribed Conic Center

It is well known that in a system of 5 random Points a unique circumscribed conic can be constructed. This conic is 5P-s-Co1 and its center is 5P-s-P1.

Construction (See Ref-19)

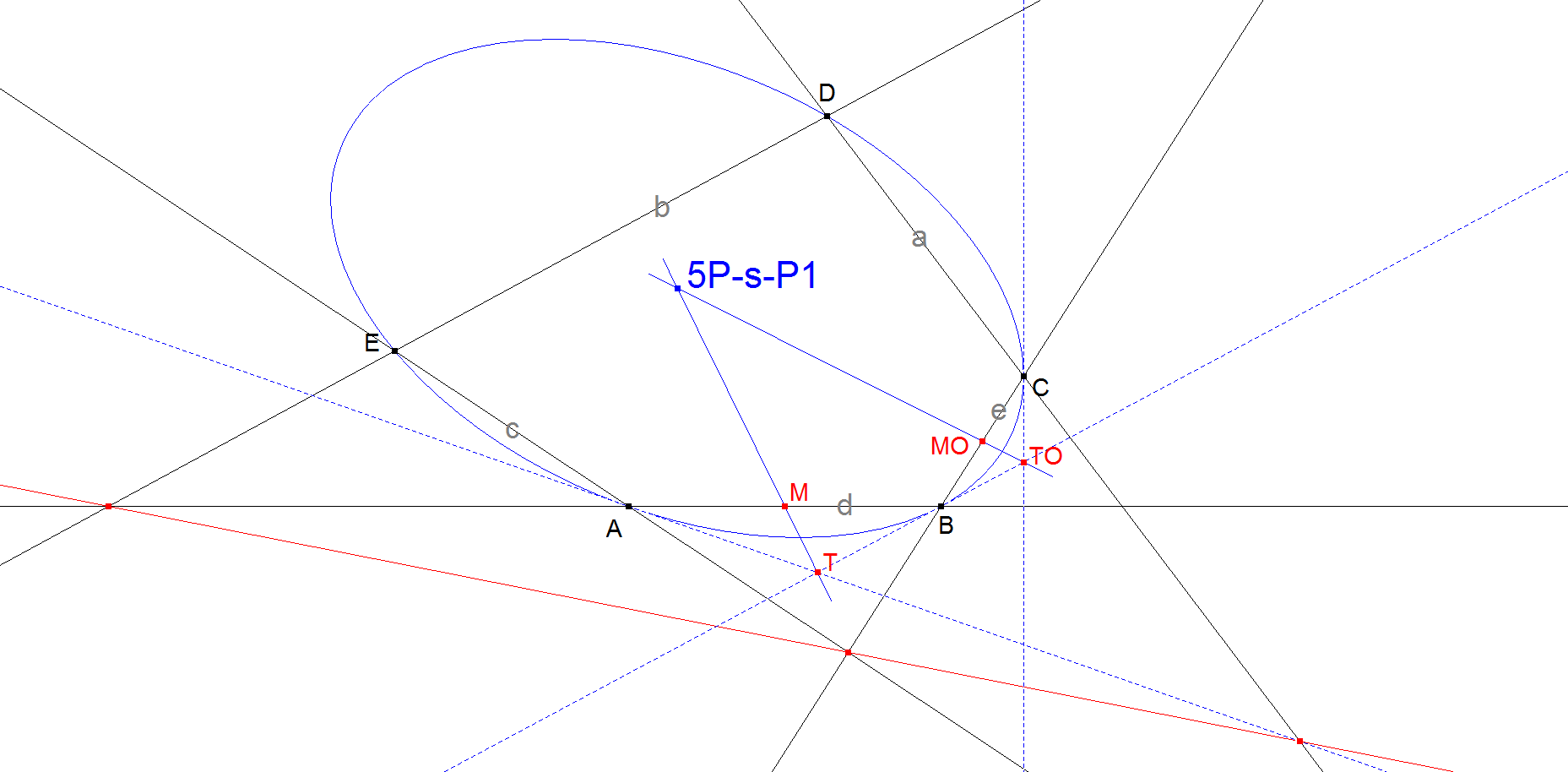
• Let the conic be defined by points A, B, C, D, E.
• Let the tangents at A, B meet at T, and those at B, C meet at TO.
• Let M, MO be the midpoints of AB and BC, then the center O is MT.MOTO.

Construction of Conic Tangents

Let d = AB, e = BC, a = CD, b = DE, c = EA, then bd.ce cuts a in a point lying on the tangent at A.

Coordinates

When using barycentric coordinates: P1=(1:0:0), P2=(0:1:0), P3=(0:0:1), P4=(p:q:r), P5=(x:y:z),

then 5P-s-P1 has coordinates:

(-p P (Q r – q R) (p P Q r + P q Q r – p P q R – p q Q R – P q r R + p Q r R) :

-q Q (P r – p R) (p P Q r + P q Q r – p P q R – p q Q R + P q r R – p Q r R) :

-(P q – p Q) r R (-p P Q r + P q Q r + p P q R – p q Q R + P q r R – p Q r R))

Correspondence with ETC/EQF

Application in Triangle Geometry:

5P-s-P1 of Pentangle ABCBr1Br2 (where Br1, Br2 are the 2 Brocard Points of Triangle ABC) is ETC Center X(8290). See [12].

Properties

• 5P-s-P1 is also the common point of the radical axes of the 5 versions of QA-Ci1 (Circumcircle of the Diagonal Triangle) in the 5-Point.
• 5P-s-P1 is also the common point of the 5 versions of QA-Co1 (Nine Point Conic) in the 5-Point.
  
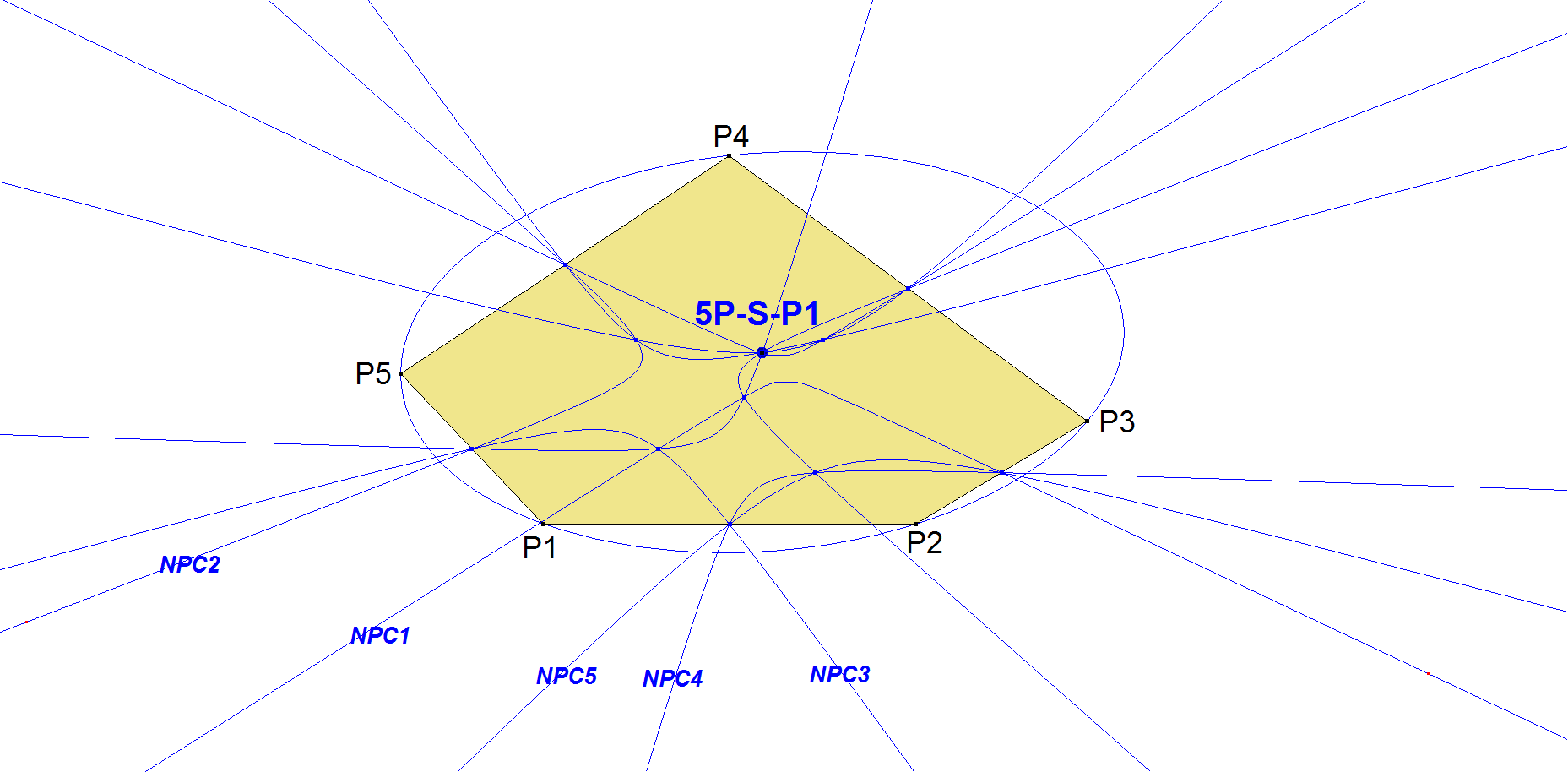
• 5P-s-Tf3(5P-s-P1) = 5P-s-P1.

Estimated human page views: 208