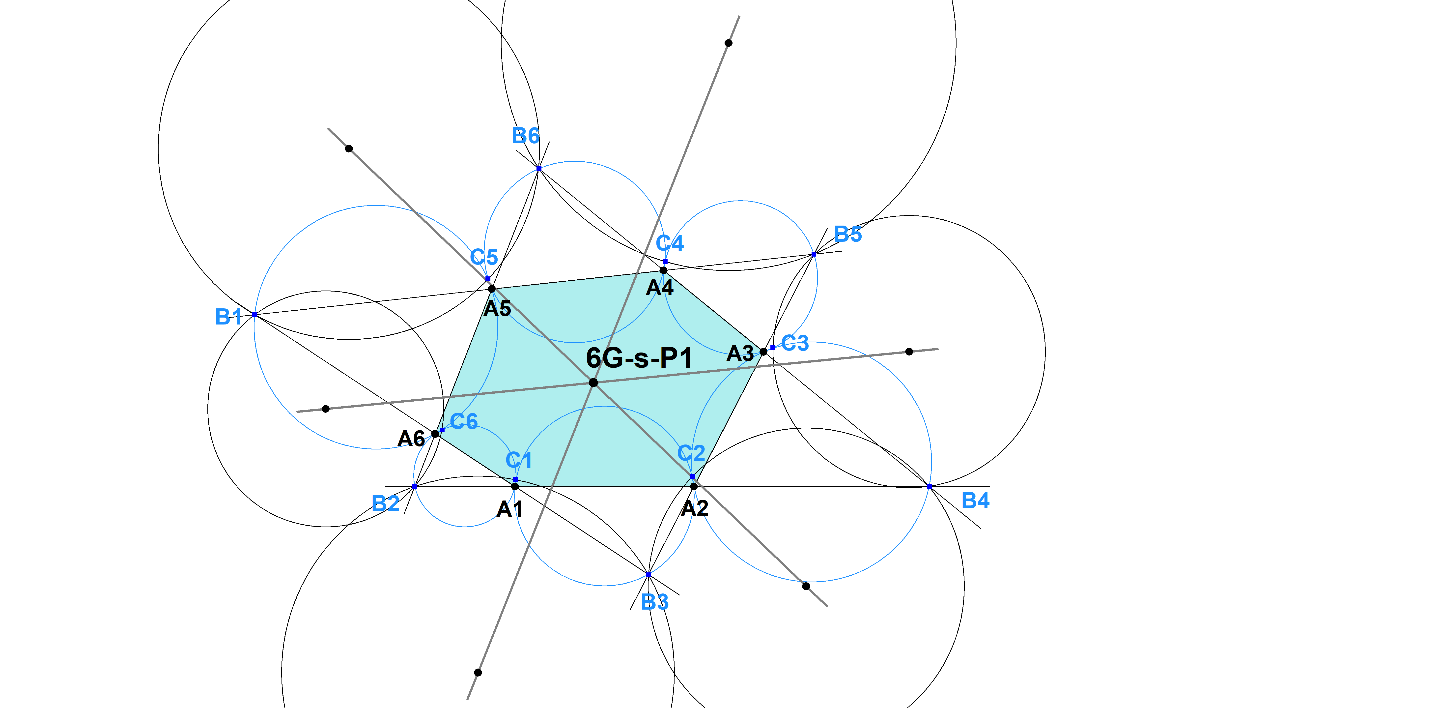
6G-s-P1 1st 6G-Hung’s Point
Let Ai, i = 1..6, be six random points.
Taking subscripts modulo 6, we denote, for i = 1.. 6,
- the intersection of the lines AiA(i+1) and A(i+2)A(i+3) by B(i+3),
- the 2nd intersection of the circumcircles of triangles AiA(i+1)B(i+2) and A(i+1)A(i+2)B(i+3) by C(i+1),
- the circumcenter of the triangle CiB(i+1)B(i+2) by Di.
- The lines D1D4, D2D5, and D3D6 are concurrent.
This 6G-point was found by Tran Quang Hung. See [34], QFG#3650.
Estimated human page views: 299
