QA-6: QA-Conversion CT → DT – coordinates

Let P1.P2.P3.P4 be the Reference Quadrangle.
Let P1.P2.P3 be the random Reference Component Triangle and let P4 be the 4th point.
The QA-Diagonal Triangle S1.S2.S3 is the Cevian Triangle of P4 wrt P1.P2.P3.
Let Q be some point to be converted from CT- to DT-coordinates.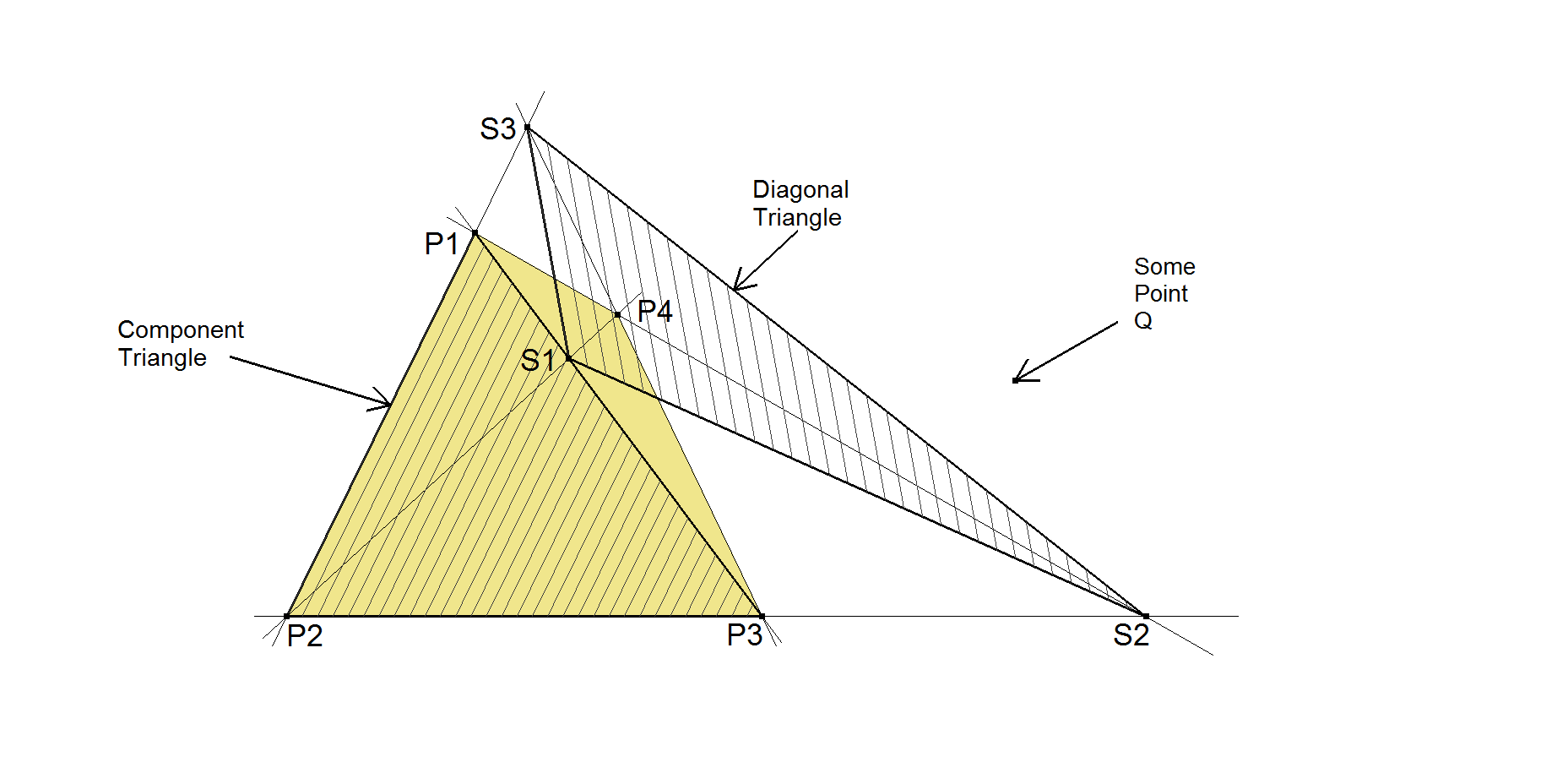
Let Qc (xc : yc : zc) be the presentation of Q in barycentric coordinates wrt the Component Triangle.
Let Qd (xd : yd : zd) be the presentation of Q in barycentric coordinates wrt the Diagonal Triangle.
Now Qc = xc·cfc1·P1 + yc·cfc2·P2 + zc·cfc3·P3 wrt the Reference Component Triangle
and Qd = xd·cfd1·S1 + yd·cfd2·S2 + zd·cfd3·S3 wrt the Diagonal Triangle,
where:
• (xc : yc : zc) are the barycentric coordinates of Q wrt the Component Triangle,
• (xd : yd : zd) are the barycentric coordinates of Q wrt the Diagonal Triangle,
• cfc1, cfc2, cfc3 are the Compliance Factors of the Component Triangle,
• cfd1, cfd2, cfd3 are the Compliance Factors of the Diagonal Triangle.

Explanation of Compliance Factors can be found at [26b page 40].
Since the Component Triangle is the Ref. Triangle, the Compliance Factors of the Component Triangle are all equal to 1.
The Compliance Factors of the Diagonal Triangle are:
• cfd1 = Det [Gd, S2, S3] / Det [S1, S2, S3]
• cfd2 = Det [S1, Gd, S3] / Det [S1, S2, S3]
• cfd3 = Det [S1, S2, Gd] / Det [S1, S2, S3]
where Gd = the Centroid of the Diagonal Triangle and “Det” is the abbreviation for “Determinant”.

Calculation gives 2 presentations of the coordinates of Q wrt the Component Triangle:
• Qc = (xc : yc : zc)
• Qd = (p(q + r)(p·yd + q·yd + p·zd + r·zd) : q(p + r)(p·xd + q·xd + q·zd + r·zd) : r(p + q)(p·xd + r·xd + q·yd + r·yd))
Since Qc and Qd present the same point we can now calculate the coordinates of Q wrt the Diagonal Triangle:
• (xd : yd : zd) = ((q + r)(qr·xc − pr·yc − pq·zc) : (p + r)(−qr·xc + pr·yc − pq·zc) : (p + q)(−qr·xc − pr·yc + pq·zc))

However, we have to bear in mind that the variables in these coordinates are expressions in (a, b, c) and (p, q, r), which are variables wrt the Component Triangle. Therefore the CT → DT-conversion of P(x : y : z) consists of 3 consecutive steps:
1. Transform Point (x, y, z) →
  ((q + r)(qr·x − pr·y − pq·z) :
   (p + r)(−qr·x + pr·y − pq·z) :
   (p + q)(−qr·x − pr·y + pq·z))
2. Replace:
  p → (−p + q + r)
  q → (p − q + r)
  r → (p + q − r)
3. Replace:
  a² → (4·p²(SA·q² + SB·q² − 2·SA·qr + SA·r² + SC·r²)) / ((p + q − r)²(p − q + r)²)
  b² → (4·q²(SA·p² + SB·p² − 2·SB·pr + SB·r² + SC·r²)) / ((p − q − r)²(p + q − r)²)
  c² → (4·r²(SA·p² + SC·p² − 2·SC·pq + SB·q² + SC·q²)) / ((p − q − r)²(p − q + r)²)

Estimated human page views: 485