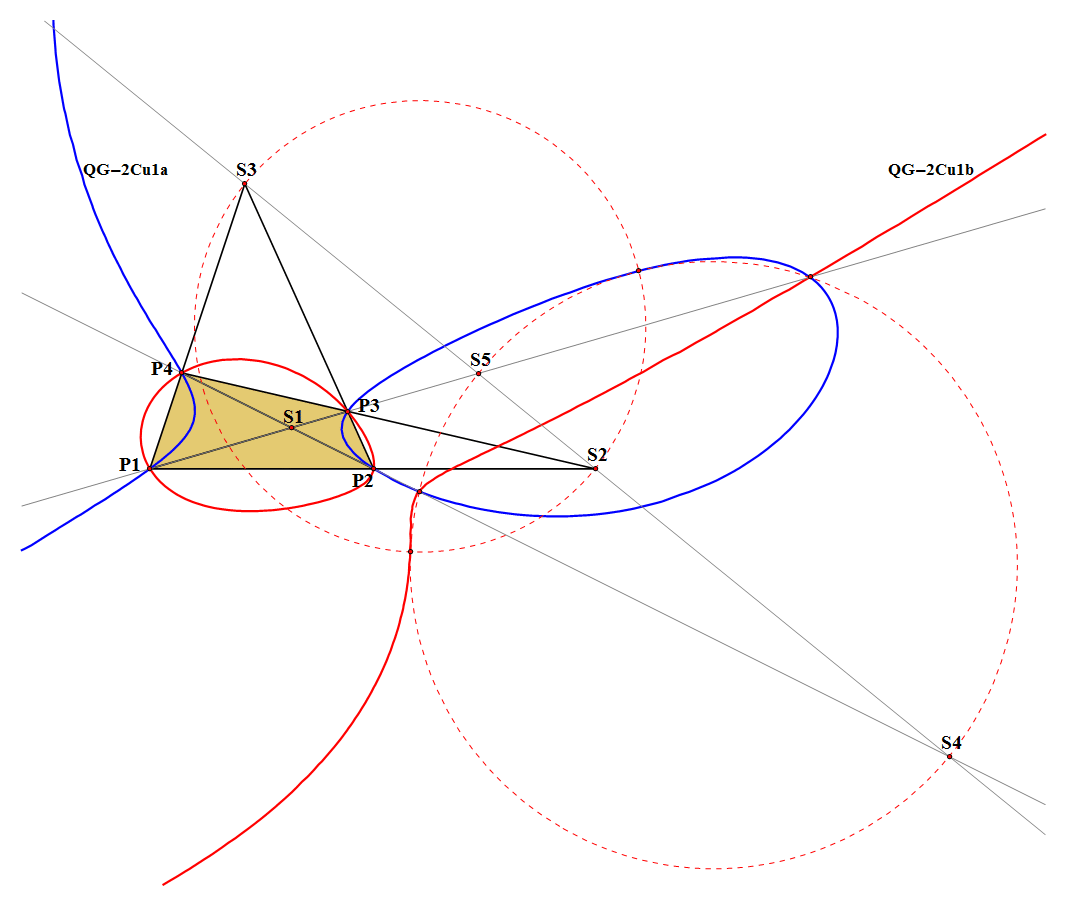
QG-2Cu1: Perspective Square Double Cubic

Eckart Schmidt discovered that the locus of perspectors of the Reference Quadrigon being point perspective with a Square comprises a double cubic: QG-2Cu1a/b.

Explanation:

It is not quite simple to construct a Square perspective with a random Quadrigon.

First of all we have to distinguish 2 types of perspectivity in the Quadri-environment:

1. Point perspectivity. This concerns 2 quadrigons from which the lines through the corresponding vertices coincide in one point called the perspector.
2. Line perspectivity. This concerns 2 quadrigons from which the intersection points of the corresponding sidelines are collinear on a line called the perspective axis (or perspectrix).

Quadrigons that are point perspective are not automatically line perspective. However when two quadrigons are line perspective they are also point perspective.

When a Reference Quadrigon is line perspective with a Square there is a very limited set of points that can function as a perspector. These points are:

1. The intersection points QG-2P4a/b of the QA-DT-Thales Circle (QG-Ci1) and the QL-DT-Thales Circle (QG-Ci2). For the construction of the corresponding line perspective squares see [34], attachment QFG-message #1240.
2. All points on the sidelines of the Reference Quadrigon, especially the vertices of the Reference Quadrigon.
3. Certain infinity points.

Equations:

CT-coordinates Equation QG-2Cu1a in 1^st QA-Quadrigon:

(r S + q SA + q SB) x² y + (r S – p SA – p SB) x y²

+ (2 q SA + r SA + r SC) x² z + (-p SA – p SC – 2 q SC) x z²

+ (-p S + r SB + r SC) y² z + (-p S – q SB – q SC) y z²

+ (-p S + r S – 2 p SA + 2 r SC) x y z = 0

CT-coordinates Equation QG-2Cu1b in 1^st QA-Quadrigon:

(r S – q SA – q SB) x² y + (r S + p SA + p SB) x y²

+ (-2 q SA – r SA – r SC) x² z + (p SA + p SC + 2 q SC) x z²

+ (-p S – r SB – r SC) y² z + (-p S + q SB + q SC) y z²

+ (-p S + r S + 2 p SA – 2 r SC) x y z = 0

DT-coordinates Equation QG-2Cu1 in 1^st QA-Quadrigon:

p r y³(c²p²-a²r²) + 2 p r y²(p² SA z-r² SC x)

-p r y((c²q²+b²r²)x²-(b²p²+a²q²)z²)

-2 p q²r x z(SA x-SC z) +q² S(x+y+z)(r²x²-p²z²) = 0

Changing the sign of S will give the other cubic. (See [34], Eckart Schmidt, QFG#2931).

Properties

• These points lie on QG-2Cu1a/b:
  • P1, P2, P3, P4: the vertices of the Reference Quadrigon lie on both cubics.
  • QG-2P4a and QG-2P4b: intersection points QG-Ci1 and QG-Ci2 (each point lying on one of both cubics).
  • QG-2P5a and QG-2P5b: intersection points QG-Ci2 and QG-Diagonals (both points lying on both cubics).
  • The infinity point of the Newton Line (lying on both cubics).
  • The two circular points at infinity (each point lying on one of both cubics).

Estimated human page views: 613