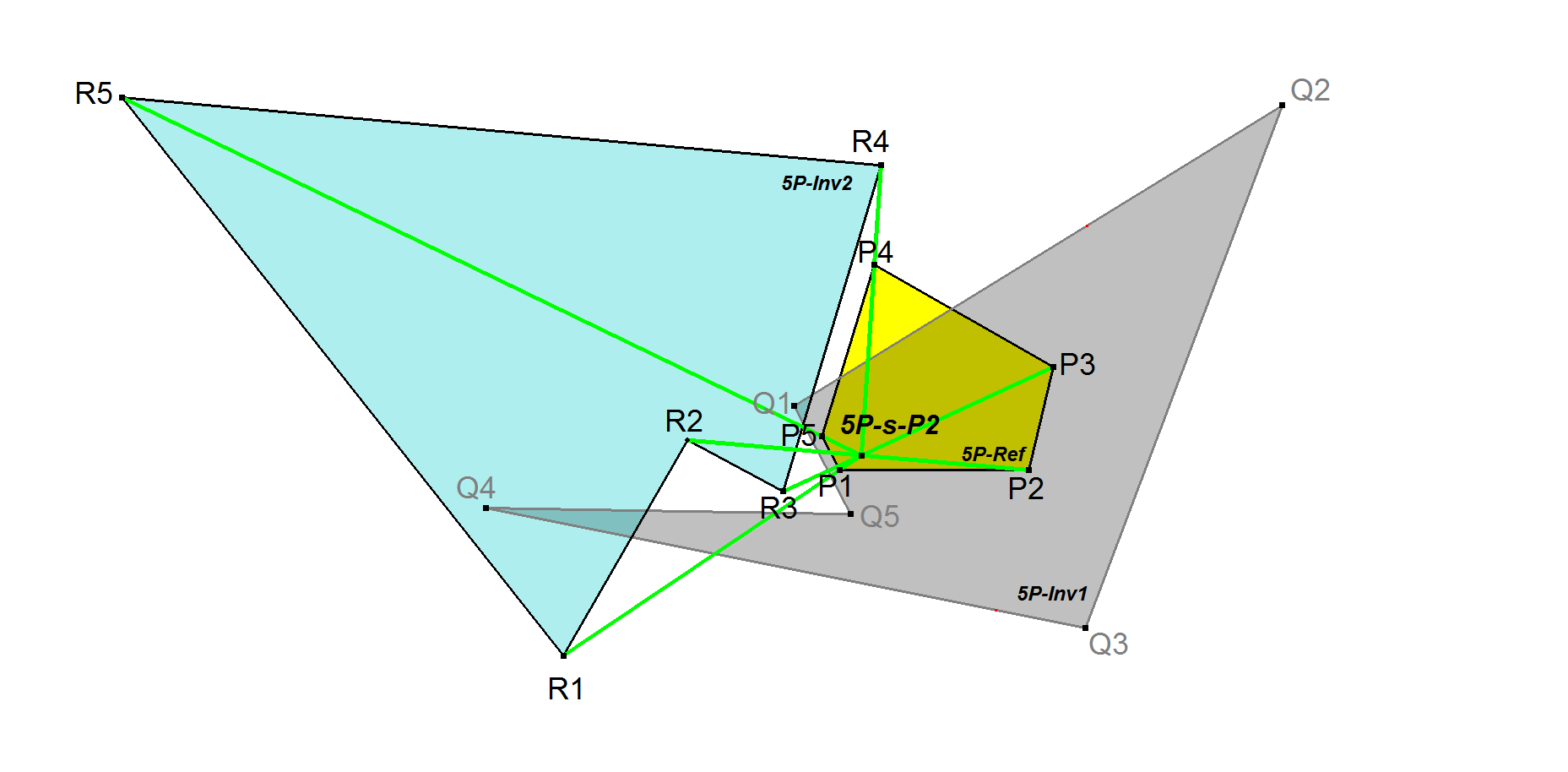
5P-s-P2: 5P-Involutary Center

Let P1.P2.P3.P4.P5 be a Pentangle (system of 5 independent random points).

Let Q1 = Involutary Conjugate (QA-Tf2) of P1 wrt Quadrangle P2.P3.P4.P5.

Let Q2 = Involutary Conjugate (QA-Tf2) of P2 wrt Quadrangle P3.P4.P5.P1.

Let Q3 = Involutary Conjugate (QA-Tf2) of P3 wrt Quadrangle P4.P5.P1.P2.

Let Q4 = Involutary Conjugate (QA-Tf2) of P4 wrt Quadrangle P5.P1.P2.P3.

Let Q5 = Involutary Conjugate (QA-Tf2) of P5 wrt Quadrangle P1.P2.P3.P4.

Next:

Let R1 = Involutary Conjugate (QA-Tf2) of Q1 wrt Quadrangle Q2.Q3.Q4.Q5.

Let R2 = Involutary Conjugate (QA-Tf2) of Q2 wrt Quadrangle Q3.Q4.Q5.Q1.

Let R3 = Involutary Conjugate (QA-Tf2) of Q3 wrt Quadrangle Q4.Q5.Q1.Q2.

Let R4 = Involutary Conjugate (QA-Tf2) of Q4 wrt Quadrangle Q5.Q1.Q2.Q3.

Let R5 = Involutary Conjugate (QA-Tf2) of Q5 wrt Quadrangle Q1.Q2.Q3.Q4.

Now Pentangle P1.P2.P3.P4.P5 is point perspective with R1.R2.R3.R4.R5.

The perspector 5P-s-P2 is a regular Pentangle Center.

5-s-P2 is the dual case of 5L-s-L2.

See [34], QFG-messages #704 and #784.

Coordinates

When using barycentric coordinates: P1=(1:0:0), P2=(0:1:0), P3=(0:0:1), P4=(p:q:r), P5=(x:y:z),

then 5P-s-P2 has these coordinates:

((-r y + q z) (p² q² r⁶ x⁶ y⁴ – p³ q r⁶ x⁵ y⁵ + 2 q⁵ r⁵ x⁸ y z – 5 p q⁴ r⁵ x⁷ y² z – 2 p² q³ r⁵ x⁶ y³ z + 5 p³ q² r⁵ x⁵ y⁴ z + 2 p⁴ q r⁵ x⁴ y⁵ z – p⁵ r⁵ x³ y⁶ z – 5 p q⁵ r⁴ x⁷ y z² + 15 p² q⁴ r⁴ x⁶ y² z² – 20 p⁴ q² r⁴ x⁴ y⁴ z² + 5 p⁵ q r⁴ x³ y⁵ z² + p⁶ r⁴ x² y⁶ z² – 2 p² q⁵ r³ x⁶ y z³ + 10 p⁴ q³ r³ x⁴ y³ z³ – 2 p⁶ q r³ x² y⁵ z³ + p² q⁶ r² x⁶ z⁴ + 5 p³ q⁵ r² x⁵ y z⁴ – 20 p⁴ q⁴ r² x⁴ y² z⁴ + 15 p⁶ q² r² x² y⁴ z⁴ – 5 p⁷ q r² x y⁵ z⁴ – p³ q⁶ r x⁵ z⁵ + 2 p⁴ q⁵ r x⁴ y z⁵ + 5 p⁵ q⁴ r x³ y² z⁵ – 2 p⁶ q³ r x² y³ z⁵ – 5 p⁷ q² r x y⁴ z⁵ + 2 p⁸ q r y⁵ z⁵ – p⁵ q⁵ x³ y z⁶ + p⁶ q⁴ x² y² z⁶  :  :  )

Properties

• 5P-s-P2 lies on a conic mentioned at 5P-s-L1.

Estimated human page views: 297