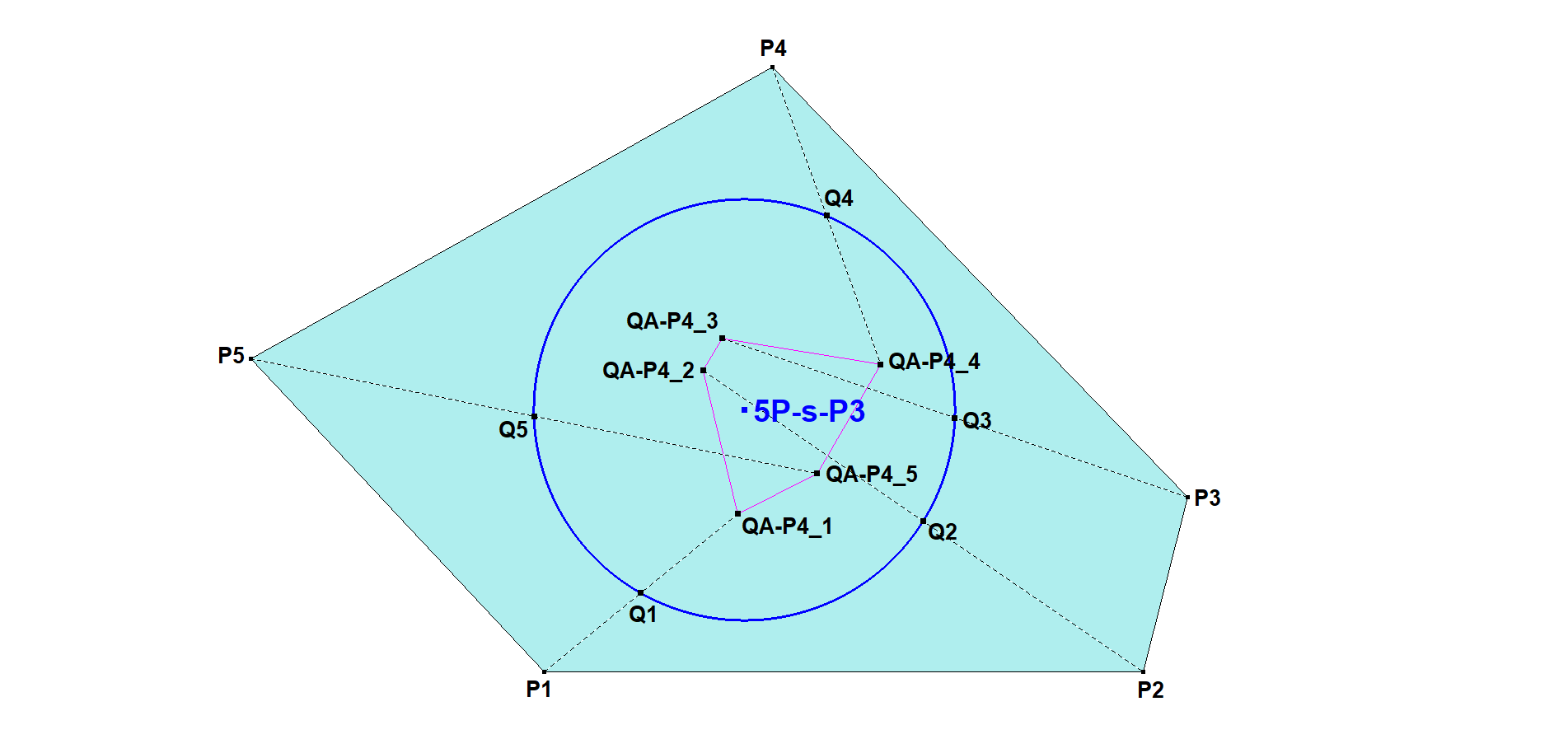
5P-s-P3 5P-Quang Duong’s Point
Let P1.P2.P3.P4.P5 be a Pentangle (system of 5 random points).
Let Q1 = Midpoint(P1, QA-P4 wrt Quadrangle P2.P3.P4.P5)
Let Q2 = Midpoint(P2, QA-P4 wrt Quadrangle P3.P4.P5.P1)
Let Q3 = Midpoint(P3, QA-P4 wrt Quadrangle P4.P5.P1.P2)
Let Q4 = Midpoint(P4, QA-P4 wrt Quadrangle P5.P1.P2.P3)
Let Q5 = Midpoint(P5, QA-P4 wrt Quadrangle P1.P2.P3.P4)
Q1, Q2, Q3, Q4, Q5 are concyclic and 5P-s-P3 is the center of the circle through Q1, Q2, Q3, Q4, Q5.
This peculiar 5P-Point was discovered by Ngo Quang Duong. See [34], QFG-messages #2773, #2774, #2777 and #2780.
Coordinates
The coordinates are too complicated to mention here.
Properties
- The midpoints of 5P-s-P4 & 5P-s-P5 and of 5P-s-P5 & 5P-s-P6 lie on Quang Duong’s circle. See [34], QFG-message #3792.
Estimated human page views: 364
