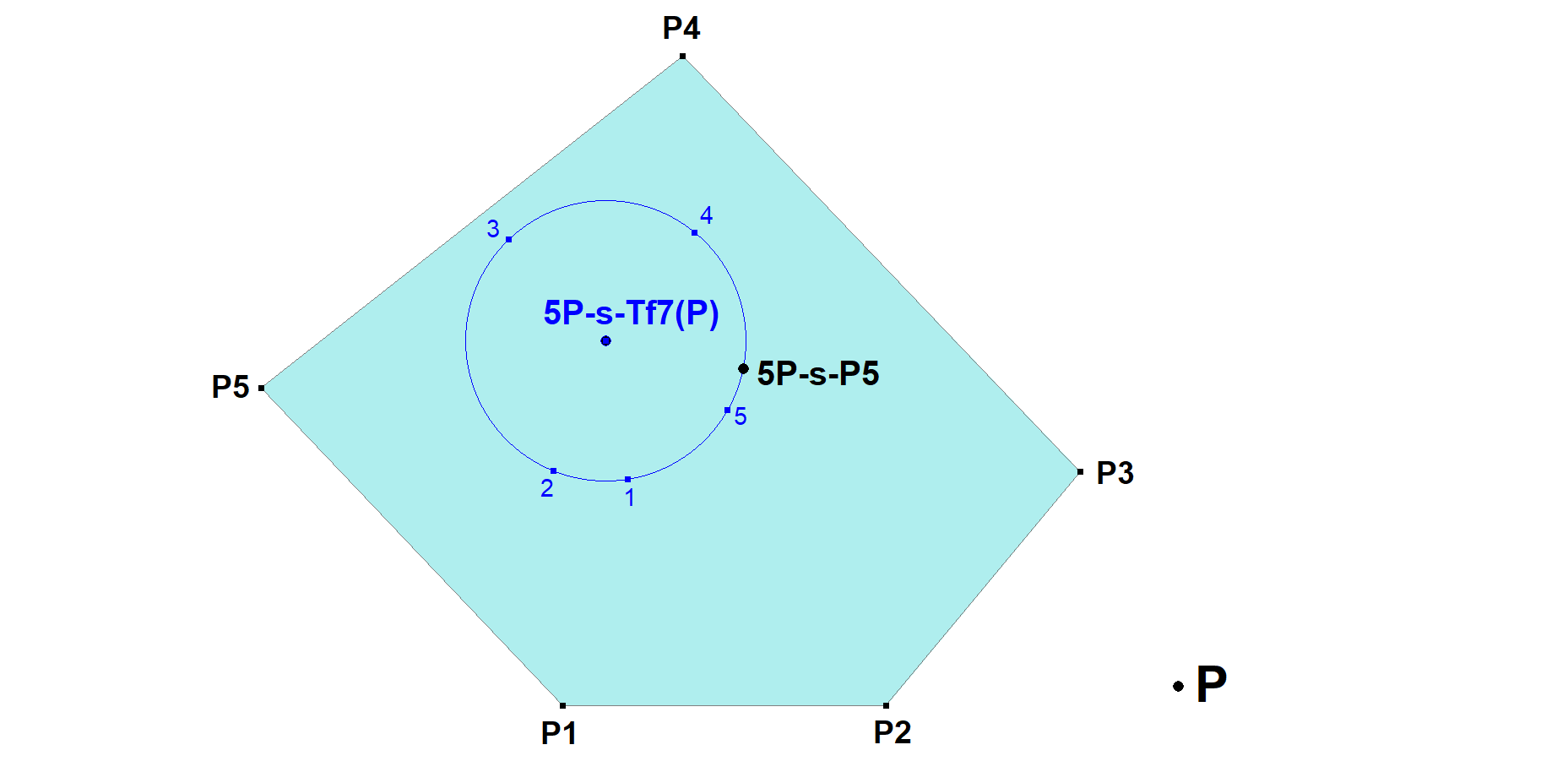
5P-s-Tf7 5P-s-P5-Circle Transformation
Let 5P be the Reference 5-Point (Pentangle) and let P be some random point.
A 5-Point contains five Component 4-Points (Quadrangles).
Consequently the combination of P with each component 4-Point will be a 5-Point having its own version of 5P-s-P5.
These 5 versions of 5P-s-P5 are concyclic with center 5P-s-Tf7(P).
This transformation is found by Eckart Schmidt and described at [34], QFG-message #3575.
Properties
- 5P-s-P5 lies on the 5P-s-Tf7(P)-circle.
- 5P-s-P5, 5P-s-P6 and 5P-s-Tf8(5P-s-P4) lie on 5P-s-Tf7(5P-s-P6). See [66], QPG-message #715.
- 5P-s-Tf7(P) = 5P-s-Tf7(5P-s-Tf6(P)). See [66], QPG-message #715.
- the 5P-s-Tf7(P)-circle degenerates to a line when P is on the 5P-curcumscribed conic.
- In a 6-Point combined with a random point P, the 5P-s-Tf7(P)-circles of the six component 5-Points concur in one point 6P-s-Tf1(P).
- Further properties can be found at [34], QFG-message #3575 and [66], QPG-message #715.
Estimated human page views: 368
