← Previous Next →

CU-2P-P1  3rd intersection point of P1P2-line

Given two random points P1 and P2 on reference cubic CU.

According to Bezout’s theorem any line (curve of 1st degree) has three intersection points with a cubic (curve of 3rd degree) in the projective complex plane. These intersection points of a line can be real or imaginary as well as finite or infinite.

Consequently, when we have 2 points P1 and P2, there will be a 3rd intersection point of the line through P1 and P2 with CU.

The existence of this point is obvious, but its construction (needed for exact positioning) is not that simple.

Infovisual CU-2P-P1-infovisual-cvt-01.png

CU-2P-P1 3rd Intersection Point with 2P-Line-01.fig

Construction

We use for the construction these cubic properties:

  1. When 2 cubics intersect in 8 points, then they will intersect in a fixed 9th point, that will be the 9th intersection point for all cubics through these 8 points. This is called the 8P-Cayley Bacharach Point CU-8P-P1. Denote CB=Cayley-Bacharach Point. See CU-8P-P1 for its construction.
  2. Given 7 points on a reference cubic CU. Then for every point Pi there will be a Cayley-Bacharach Point CBi(P1,…,P7,Pi) with special property that 3rd intersection point P.CBi with CU will be fixed for every general location of Pi. This point is called CU-7P-P1, the 7P-Pivot Point. See CU-7P-P1 for its construction.
  3. When 2 cubics intersect in 9 points and 3 are collinear then the other 6 will be coconic.
  4. When 2 cubics intersect in 9 points and 6 are coconic then the other 3 will be collinear.

Now we can proceed to the actual construction:

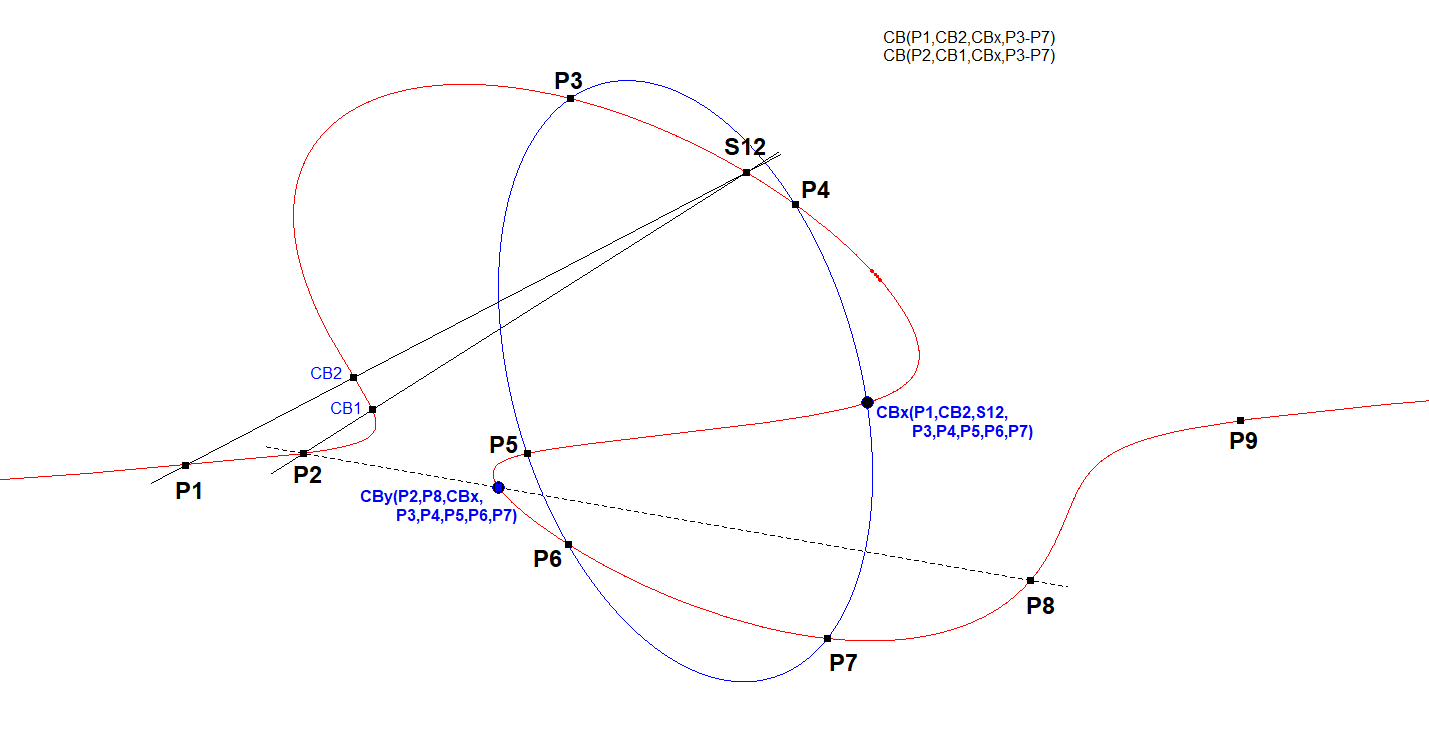
  1. Determine 9 points P1, …, P9 on the cubic.
  2. Construct CB1=CB(P2,P3, …, P9) and CB2=CB(P1,P3, …, P9). Lines P1.CB2 and P2.CB1 will meet in 7P-Pivot Point S12 on CU.
  3. Construct CBx=CB(P1,CB2,S12,P3,P4,P5,P6,P7). The first three points are collinear, therefore CBx will be the 6th intersection point of conic(P3,P4,P5,P6,P7).
  4. When we want to know the 3rd intersection point of P2.P8 then this will be CBy = CB(P2,P8,P3,P4,P5,P6,P7), because the last 6 points are coconic. The points P2 and P8 can be replaced by random points Px, Py.
  5. So we have a method for finding the 3rd intersection point of PxPy with CU given 9 help points on CU.

There is another construction described at [Cuppens, pages 243,244].



Estimated human page views: 5

Scroll naar boven