CU-4P-P2 CB4d-Point
Given a general reference cubic CU and 4 random points (P1,P2,P3,P4) on it.
A situation is conceivable that two or more cubics are mutually tangent at these 4 points.
All P1-P2-P3-P4-circumscribed cubics sharing the same tangent at P1, P2, P3 and P4 have a common point CB4d. It is a special case of the Cayley-Bacharach Theorem (see CU-8P-P1) for general cubics circumscribed about a quadrangle.
See QPG#839 (attachment §3.10) and QPG#794-814 for more information.
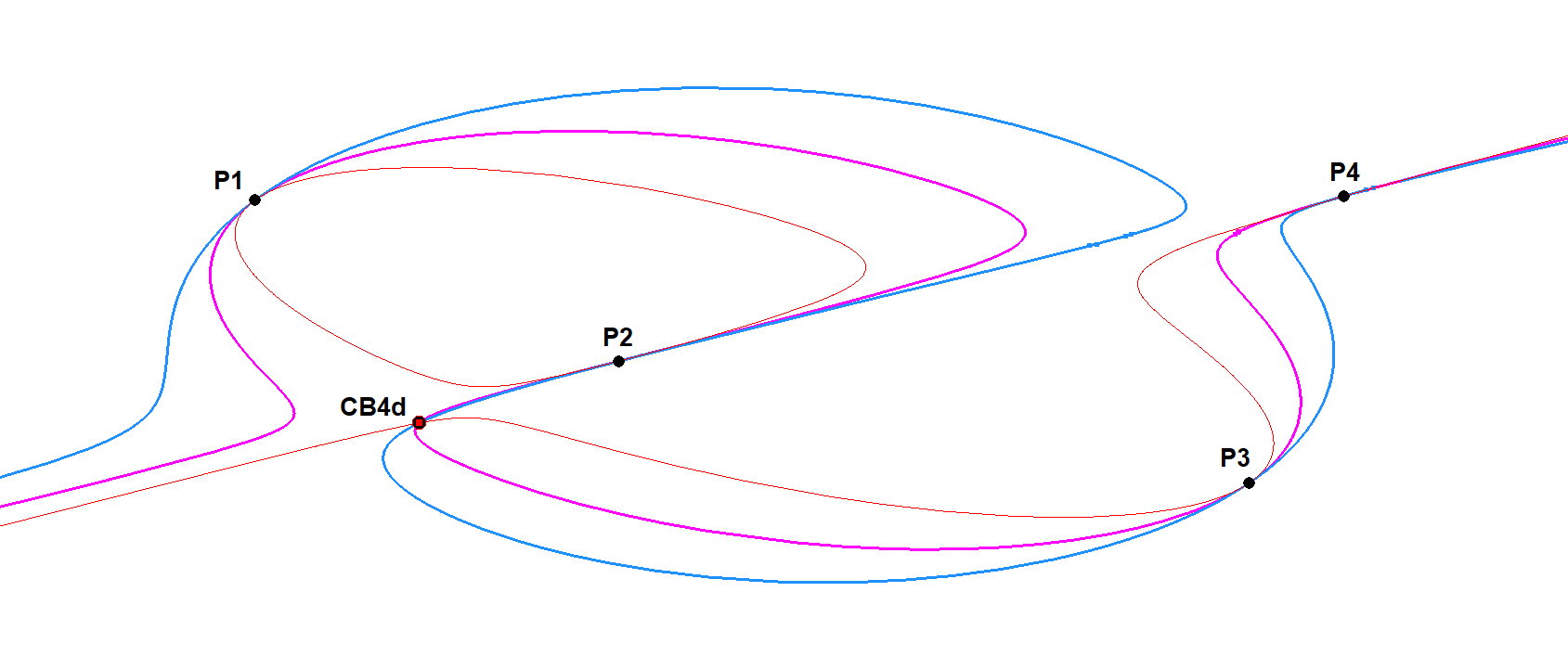
CU-4P-P2 CB4d-Point-01.fig
Circular Cubics
When the reference cubic is a circular cubic then 3 random points with mutually tangent cubics at these points produce a CB3d-point. This is a special case of the Cayley-Bacharach Theorem (see CU-8P-P1) for circular cubics circumscribed about a triangle.
Relationship with CTC and ETC
The point CB3d on the Neuberg cubic K001 is X(2133). See QPG#797.
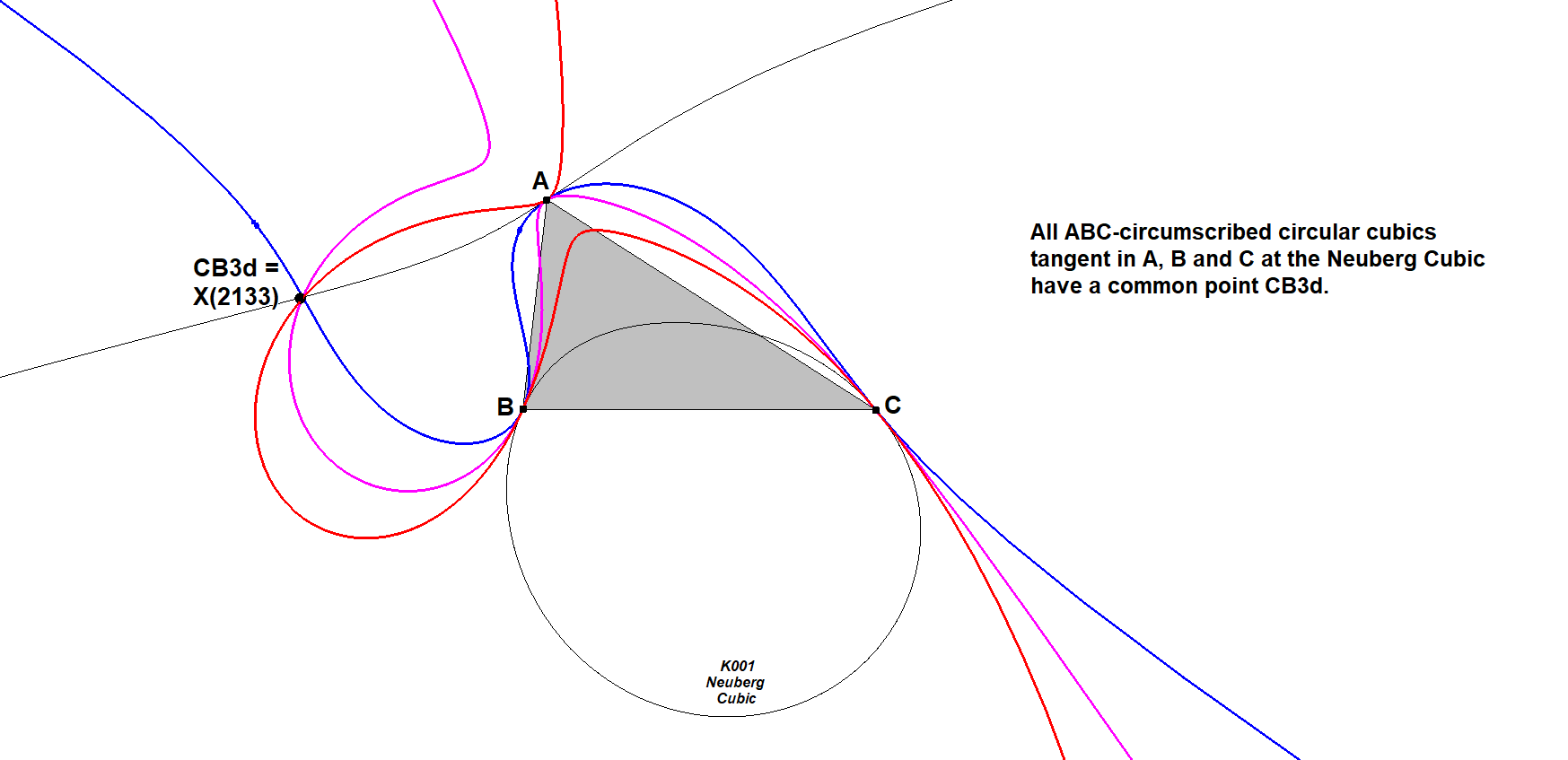
CU-4P-P2 CB4d-Point-Case Neuberg Cubic-10.fig
Relationship with EQF
The point CB4d on the cubic QA-Cu1 is the tangential of QA-P41. See QPG#800.
Estimated human page views: 57
