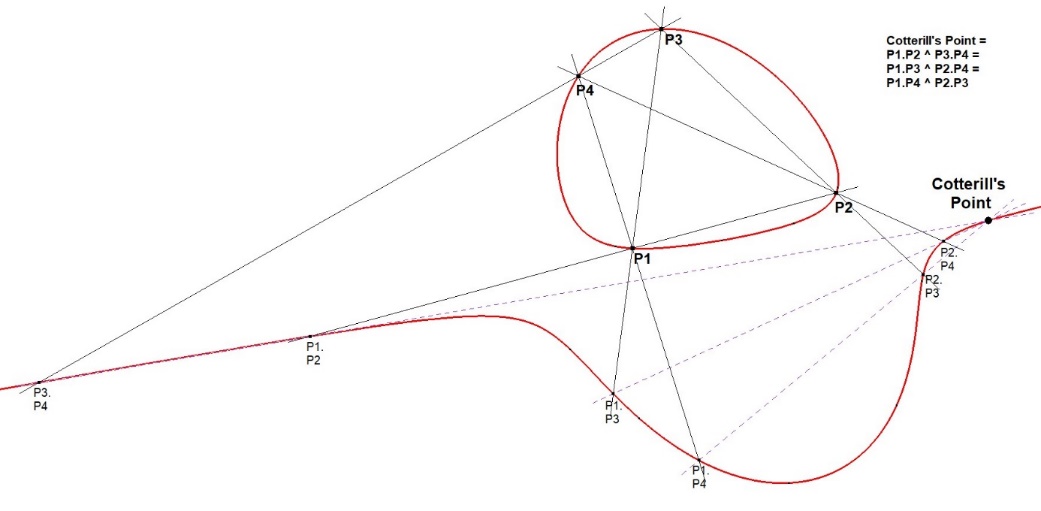
CU-4P-P1 Cotterill’s Point
Definition
Let Px and Py be points on the cubic curve CU, and denote (Px.Py) as the third point of intersection of the line PxPy and the curve CU.
The Cotterill’s Point associated with four points P1, P2, P3, P4 on CU is defined as
(P1.P2).(P3.P4).
However it is also equal to
(P1.P3).(P2.P4) and (P1.P4).(P2.P3).
This invariance under pairings makes it a ditinguished point.
Historical Content
Cotterill’s Point is known from these papers:
1. Thomas Cotterill himself published in 1851:
A Geometrical Property of Curves of the third Order, The Cambridge and Dublin Mathematical Journal, Vol VII, p.14, 1851. See [78]
2. H. Durège used the terminology “gegenuberliegende Punkt” and published in 1871:
Die Ebenen Curven Dritter Ordung, Leipzig, 1871. See [84].
3. R. Deaux used the word “coresidual” and published in 1953:
Cubiques anallagmatiques, Mathesis, 62 (1953) 193–204
It looks like Cotterill was the first one to publish about this point.
CU Point Validation
- (P1.P2).(P3.P4) = N – (N-P1-P2) – (N-P3-P4) = P1+P2+P3+P4 – N,
- (P1.P3).(P2.P4) = N – (N-P1-P3) – (N-P2-P4) = P1+P2+P3+P4 – N,
- (P1.P4).(P2.P3) = N – (N-P1-P4) – (N-P2-P3) = P1+P2+P3+P4 – N,
which proves that these three construction methods (P1.P2).(P3.P4), (P1.P3).(P2.P4), (P1.P4).(P2.P3) yield a point of identical value.
So CU-4P-P1 = PP4 – N.
Properties
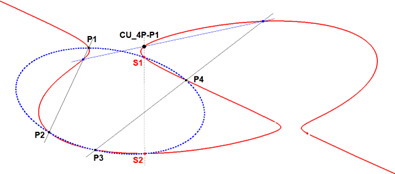
- Every Conic passing through 4 given points on a cubic will cut it again in 2 points (accoring to Bezout’s Theorem), such that the straight line joining them will pass through a fixed point being Cotterill’s point. See [78].
Estimated human page views: 64
