CU-7P-P1 CB-Pivot Point
Definition
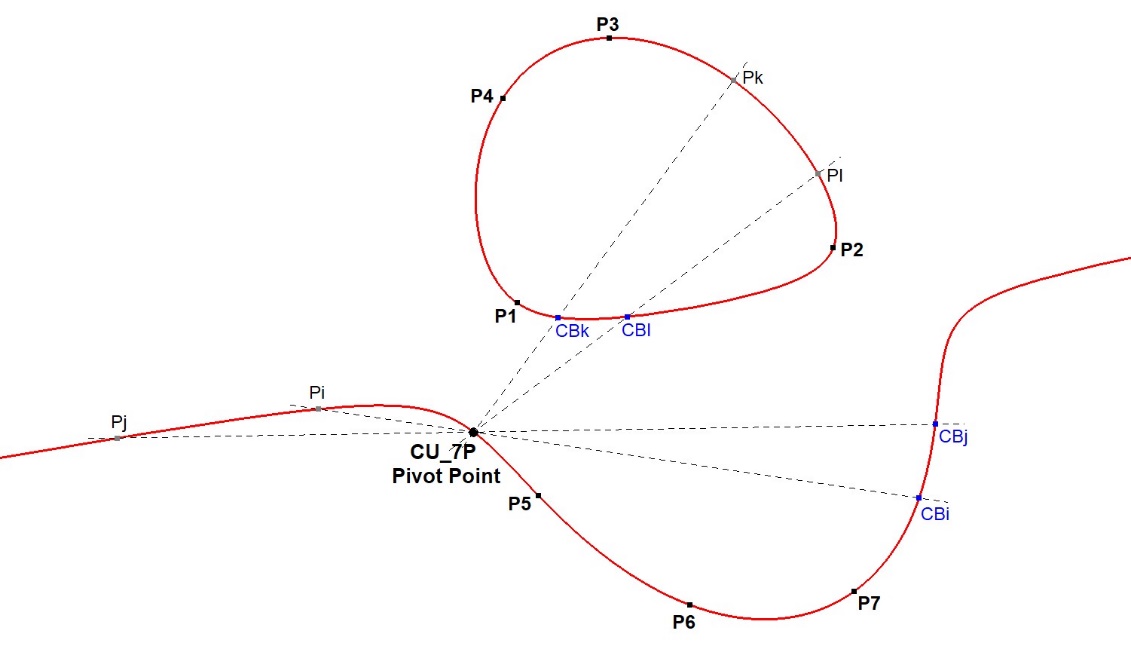
- Given a fixed set of 7 random reference points Pi (i=1, …, 7) on CU.
- Given two extra random points Px and Py on CU.
- Every set of 8 points define a Cayley-Bacharach Point (CU-8P-P1) of these 8 points.
- We can compose two sets of 8 points by adding Px and Py to the fixed set of 7 points.
- Let CBx be the CB-point of (P1, …, P7,Px) and CBy be the CB-point of (P1, …, P7,Py).
- The intersection point of lines PxCBx and PyCBy will appear to be a fixed point on CU.
- This point is the CU-Pivot Point.
This point was contributed by Eckart Schmidt.
It is a unique point on CU determined by just 7 reference points on CU.
CU Point Validation
- Pi.Pj=(Pi+Pj)-N and CBi=3N-(PP9-Pi);
- Let Tx=Px.CBx, then Tx=(Px+(3N-(PP7+Px))-N)=2N-PP7
- Let Ty=Py.CBy, then Ty=(Py+(3N-(PP7+Py))-N)=2N-PP7
- Tx and Ty are constructed both as a point on CU and are identical points since they have the same validation. So CU-7P-P1 = 2N – PP7.
- From the formula it is clear that this point is independent of Px and Py, since they do not appear in the formula.
Estimated human page views: 72
