CU-Ci1 The unique CU-Polar Circle

There exists one and only one point X for which the X-Polar Conic (CU-P-Co1) is a circle.

Proof:

Since a Polar Conic wrt a Cubic at X(p,q,r) algebraically is derived from:

(D[Cubic, x], D[Cubic, y], D[Cubic, z]) . (p,q,r)

we have a linear equation in (p,q,r) when (x,y,z) is substituted by the coordinates of the circular points at infinity CI1 or CI2.

Consequently the 2 substitutions with CI1 and Ci2 will give 2 linear equations in (p,q,r).

Both equations must satisfy for a point X having a circular X-Polar Conic, so only the intersection point of both conditional lines coming forth from these 2 equations will give a circular X-Polar Conic.

So there is always one and only one point X for which the X-Polar Conic wrt a cubic is a circle.

CU-Ci1 Unique Polar Circle of a Cubic-01.jpg

References

See QPG#2322-2324 and [Gibert, Isocubics, page 21].

Properties

• When the Reference Cubic is a Circular Cubic (CUc), then X will be the Singular Focus of CUc.
• If the cubic has three real asymptotes, then X is the Lemoine point aka Symmedian Point (X(6) in the Encyclopedia of Triangle Centers) of the triangle formed by the asymptotes and, obviously, when they concur, it is the point of concurrence. See [Gibert, Isocubics, page 21].
• The parallels to these asymptotes passing through X meet the cubic again at six points lying on a related circle. This circle is the first Lemoine circle of the Asy-triangle CU-3L1. See [Gibert, Isocubics, page 21].

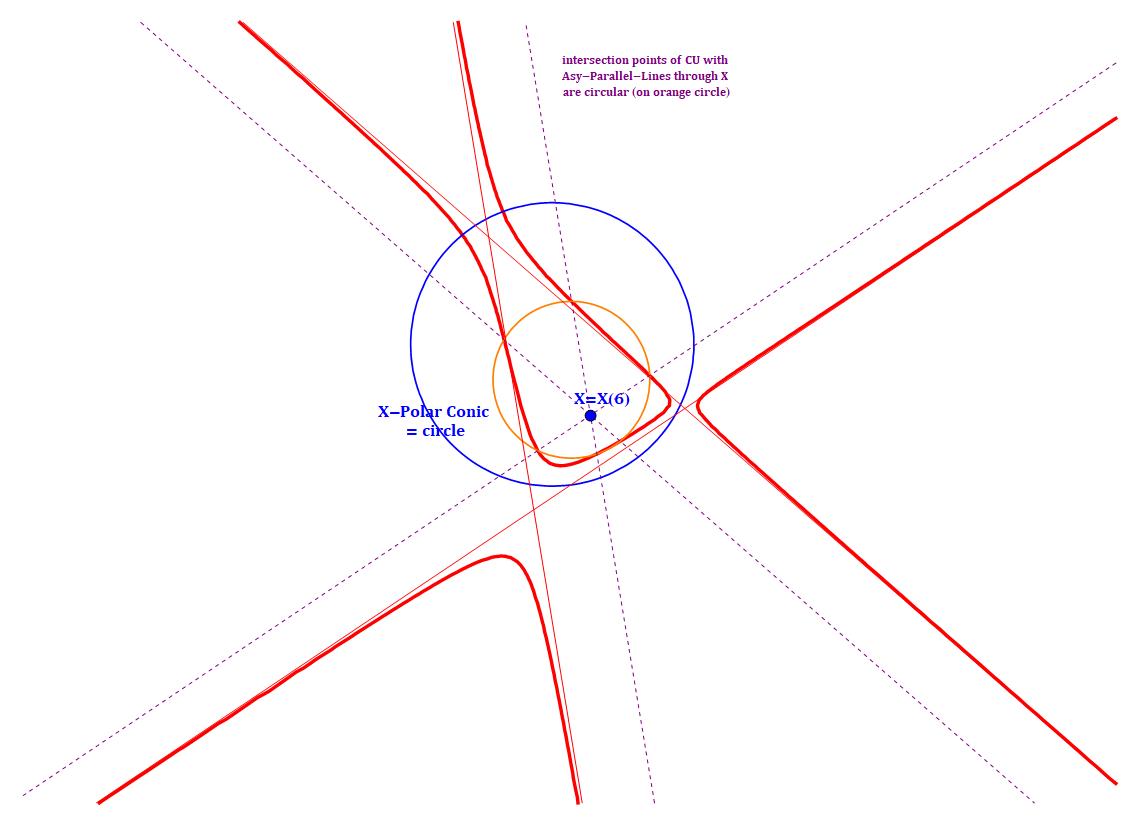
CU-Ci1 Unique Polar Circle of a Cubic-02.jpg

Estimated human page views: 17