CU-P-Tf2 1^st CU-P Transformation

Given a Reference Cubic CU and a random reference point P on the cubic.

• Let X, Pa, Pb, Pc be four random points on CU.
• Let Sa, Sb, Sc be the 3^rd intersection points of CU and resp. PPa, PPb, PPc.
• Construct conics (X, Pa, Sa, Pb, Sb), (X, Pa, Sa, Pc, Sc), (X, Pb, Sb, Pc, Sc). These conics will be shown to concur in a common cubic point Y=CU-P-Tf2(X), which is independent of Pa, Pb, Pc.

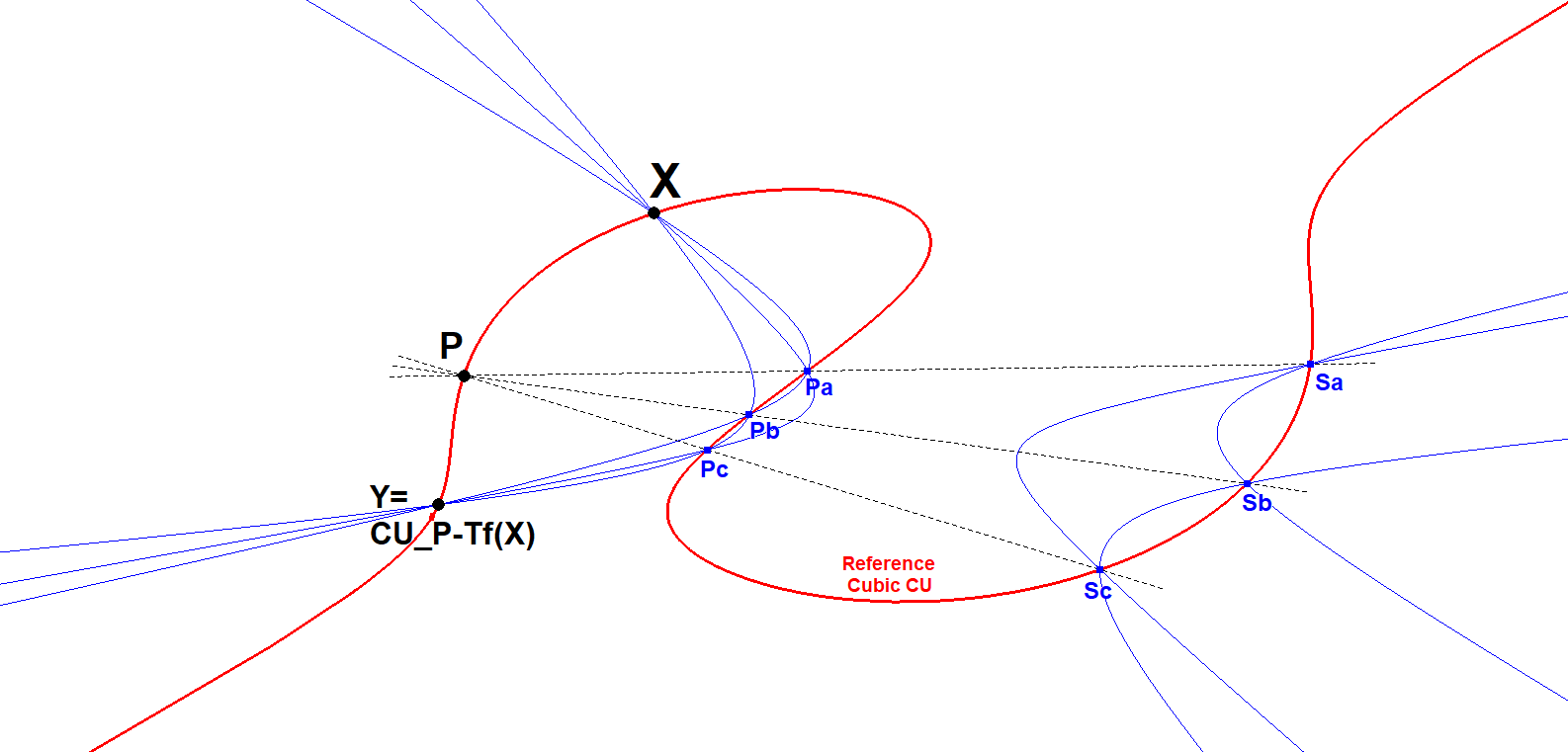
CU Point Validation

• Lines:  P+Pa+Sa=N,   P+Pb+Sb=N,   P+Pc+Sc=N
• Conic: X+Pa+Sa+Pb+Sb+Y=2N  –>  X+Pa+(N-P-Pa)+Pb+(N-P-Pb)+Y=X+2N-2P+Y=2N  –>  Y=2P-X

This validation shows that transformation point Y is a point on CU independent of Pa,Pb,Pc,Sa,Sb,Sc.

Properties

• Let Z be 3^rd intersection point of the CU-cubic with line XY: Z+X+Y=N.
• Subsititute Y=2P-X Z+X+2P-X=N Z+2P=N, which shows that the 3 points Z,P,P are collinear and therefore Z is the tangential of P.

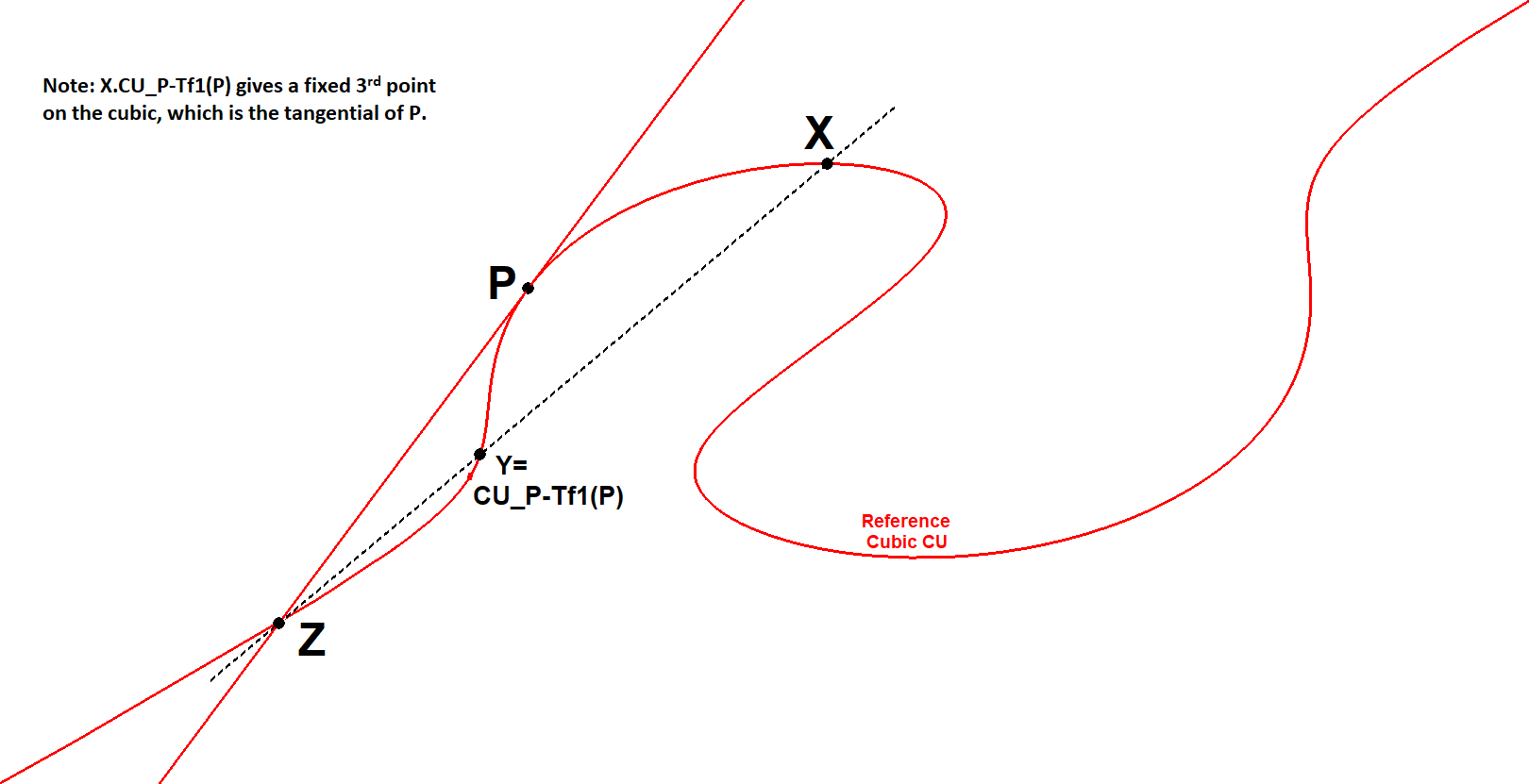
Construction of P-tangent and P-tangential

• This gives a construction method for the tangent at some point P1 to the cubic as well as the tangential of that point P0 on the cubic.
• Let P be some point on the cubic for which we want to construct the tangent.
• Let X, Pa, Pb, Pc be four random points on the cubic.
• Let Sa,Sb,Sc be the 3^rd intersection points of PPa,PPb,PPc with the cubic.
• Let Y be the 4^th intersection point of the conics (X,Pa,Sa,Pb,Sb) and (X,Pa,Sa,Pc,Sc).
• Let Z be the 3^rd intersection point of XY with the cubic.
• Z will be the tangential of P0 wrt the cubic and PZ will be the tangent at P to the cubic.

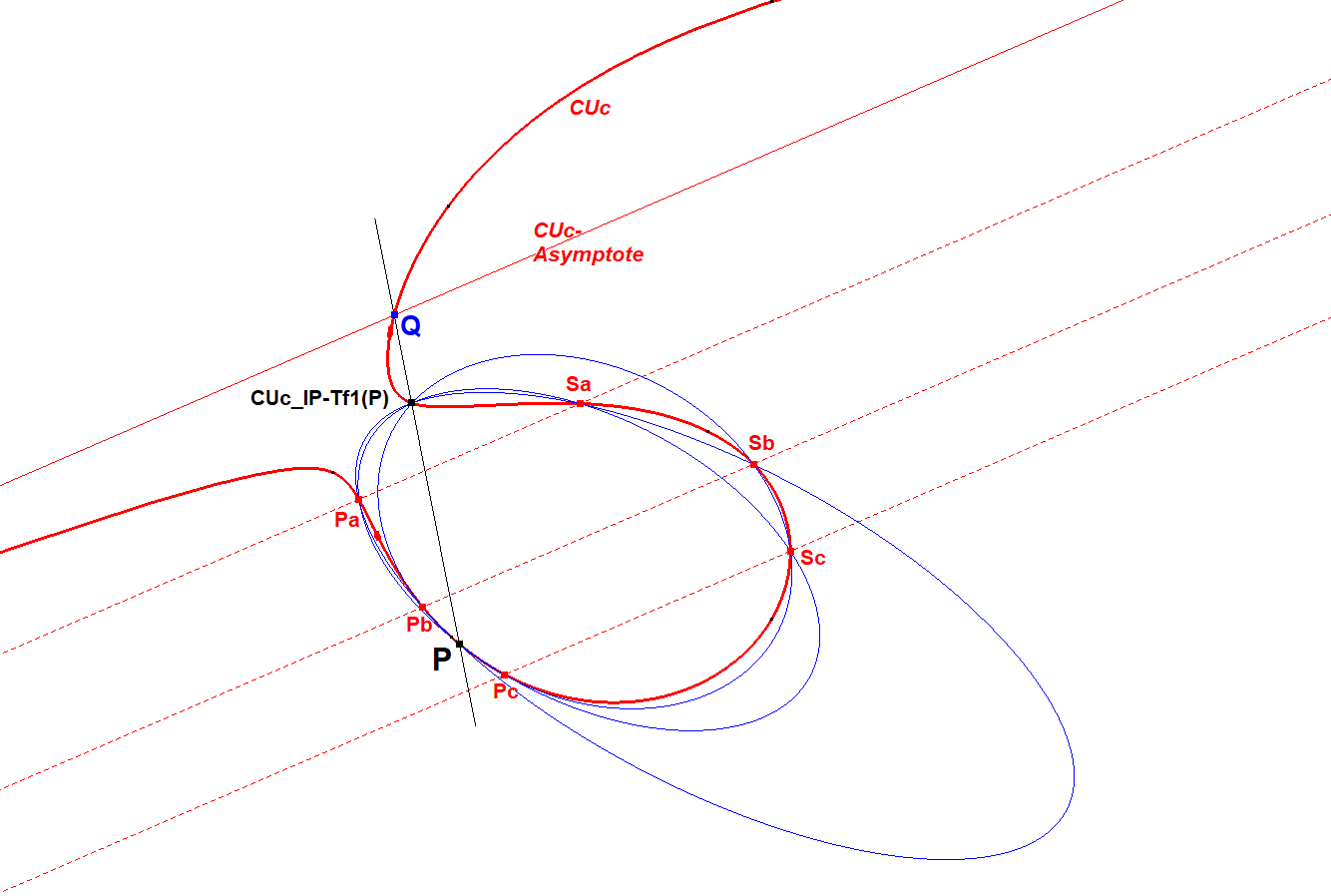
Another Property

• When the cubic is cicular and the fixed point is IP (infinity Point), then CU-P-Tf1(P)=Q=intersection point of asymptote with CUc. This offers a method to contruct Q, the intersection point of the CUc-asymptote with CUc.

Estimated human page views: 6