CU-IP-4P1 Anallagmatic Points

Anallagmatic means: without change (from the Greek allagma “change”).

A curve is said to be anallagmatic if it is globally invariant by an inversion, meaning that the inversion of a point on the curve will be another point on the curve.

This notion was studied by Moutard in 1864.

Normally an inversion is related to an inversion-circle. However here we also consider the inverse of a point X wrt an inversion-conic. One might call this a ‘quasi-inversion’ and the conic center a ‘quasi-anallagmatic point’.

The (quasi-)inverse of P wrt inversion-conic CO with center O is constructed as follows: Draw a half-line OP and let S be the intersection point of OP with CO. Now construct X such that OS²=OP*OX.

It is said that all Circular Cubics are Anallagmatic Curves, meaning that there are circle center(s) on the curve for which its circle functions as an inversion-circle. Every point on the curve inverted wrt this inversion-circle will result in another point on the curve.

Picture of 2 Anallagmatic Points on a Circular Cubic working with inversion-circles

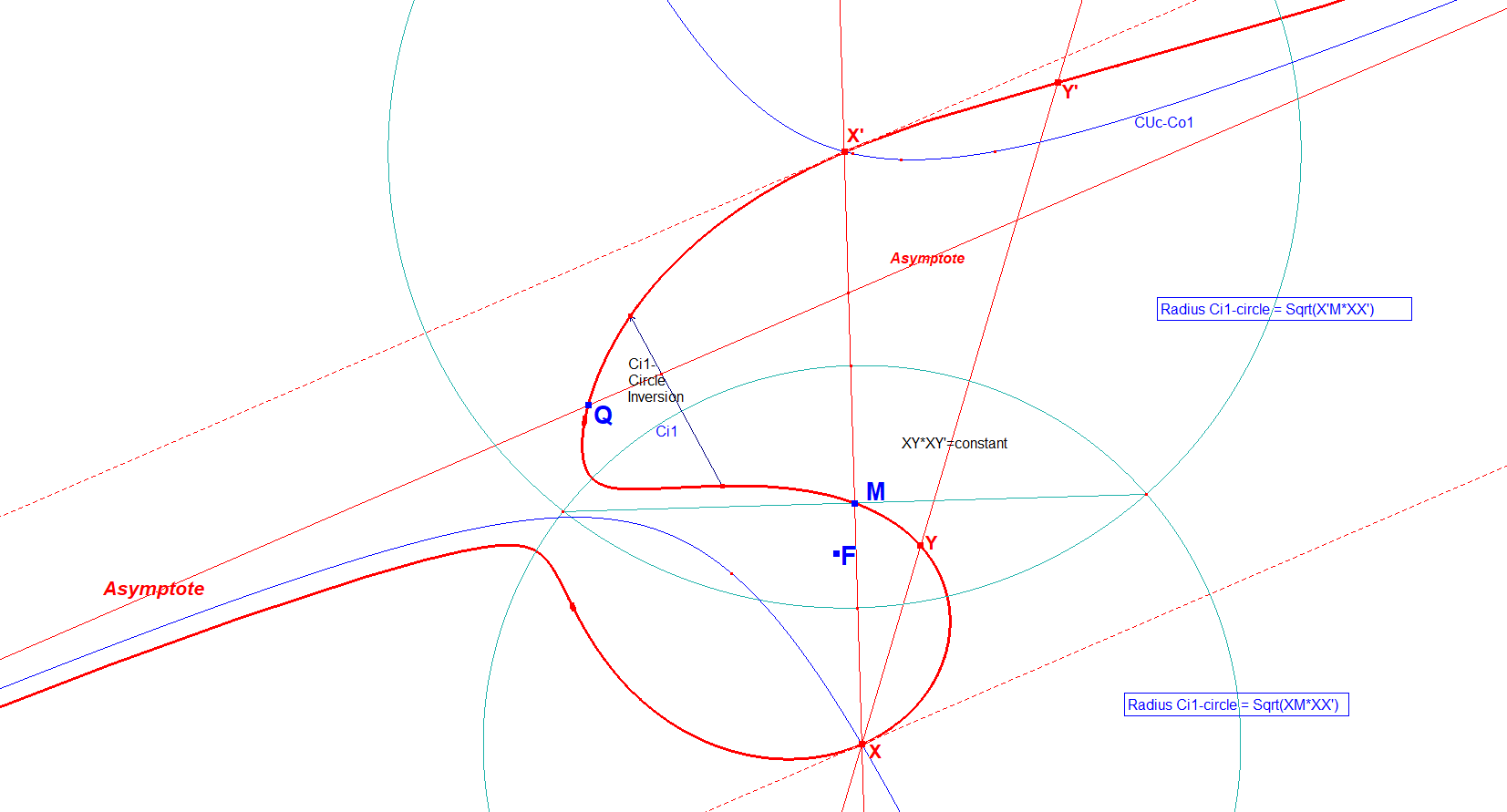
CUc1-Tf1-MonopartiteCubic-CSC Moebius Trf-28-Anallagmatic property.fig

General rules for Anallagmatic points

1. Strictly speaking, anallagmatic points on a cubic only occur on circular cubics.

2. However, there is a quasi-variant occurring on regular non-circular cubics. Instead of inversion-circles, there will be inversion-conics.

3. In general, a cubic has 3 asymptotes, two of which can be imaginary.

4. Per asymptote there are 4 anallagmatic points, of which 2 can be imaginary in the case of a real asymptote. All of them will be imaginary in the case of imaginary asymptotes. Ultimately, it is therefore possible that a cubic ends up with just 2 real anallagmatic points (case of a monopartite cubic). But it is also possible there will be 3×4 real anallagmatic points (case of a tripartite or quadripartite cubic).

5. Since there are always per asymptote 4 anallagmatic points, we talk here about an Anallagmatic Quadrangle, bearing in mind that 2 or even 4 of them can be imaginary. In the extreme case we even are dealing with an imaginary quadrangle.

General construction of Anallagmatic points

1. Given a reference cubic CU.
2. This cubic has 3 asymptotes, at least one of which is real.
3. Choose a real CU-Asymptote.
4. There are 4 points P1, P2, P3, P4 on the cubic where the tangent is parallel to this asymptote. These 4 points are called the anallagmatic points. Two of them can be imaginary points, for example on a monopartite cubic, leaving only 2 real anallagmatic points.
5. They are the intersection points of CU with the Diametral Conic (CU-IP-Co1) corresponding with the chosen CU-asymptote. This is because the Diametral Conic is a P-Polar Conic and a P-Polar Conic intersects the cubic at the points of tangency of all possible tangents to P. Clearly, P here is the CU- infinity point of the chosen asymptote.
6. The Diametral Conic is a Hyperbola sharing an asymptote with the chosen CU-Asymptote.
7. Cubic and Hyperbola are mutually tangent at their common infinity point, making this point a double intersection point of both curves. According to Bezout’s Theorem there are 6 intersection points of a conic and a cubic and therefore 4 finite intersection points remain and these are the Anallagmatic points Pi (i=1,2,3,4).
8. When there are 3 real asymptotes, then there will be 3 different sets of 4 Anallagmatic Points (Anallagmatic Quadrangles), in sets of 2 possibly being imaginary points.

Picture Anallagmatic Points on a Monopartite Cubic

There is 1 real asymptote and there are just 2 real Anallagmatic Points.

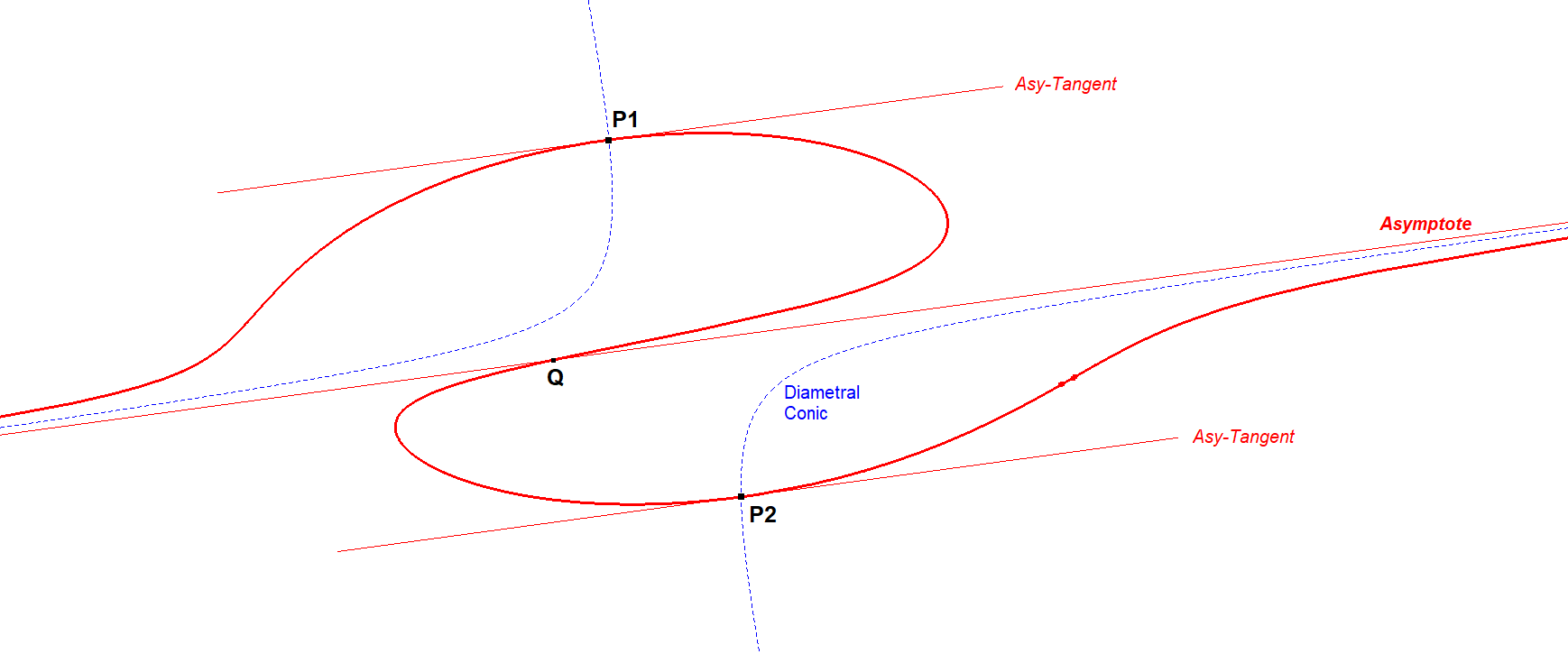
CU1-Monopartite Cubic-04-Anallagmatic Points.fig

Picture Anallagmatic Points on a Bipartite Cubic

There is an example with 1 real asymptote and there are 4 real Anallagmatic Points.

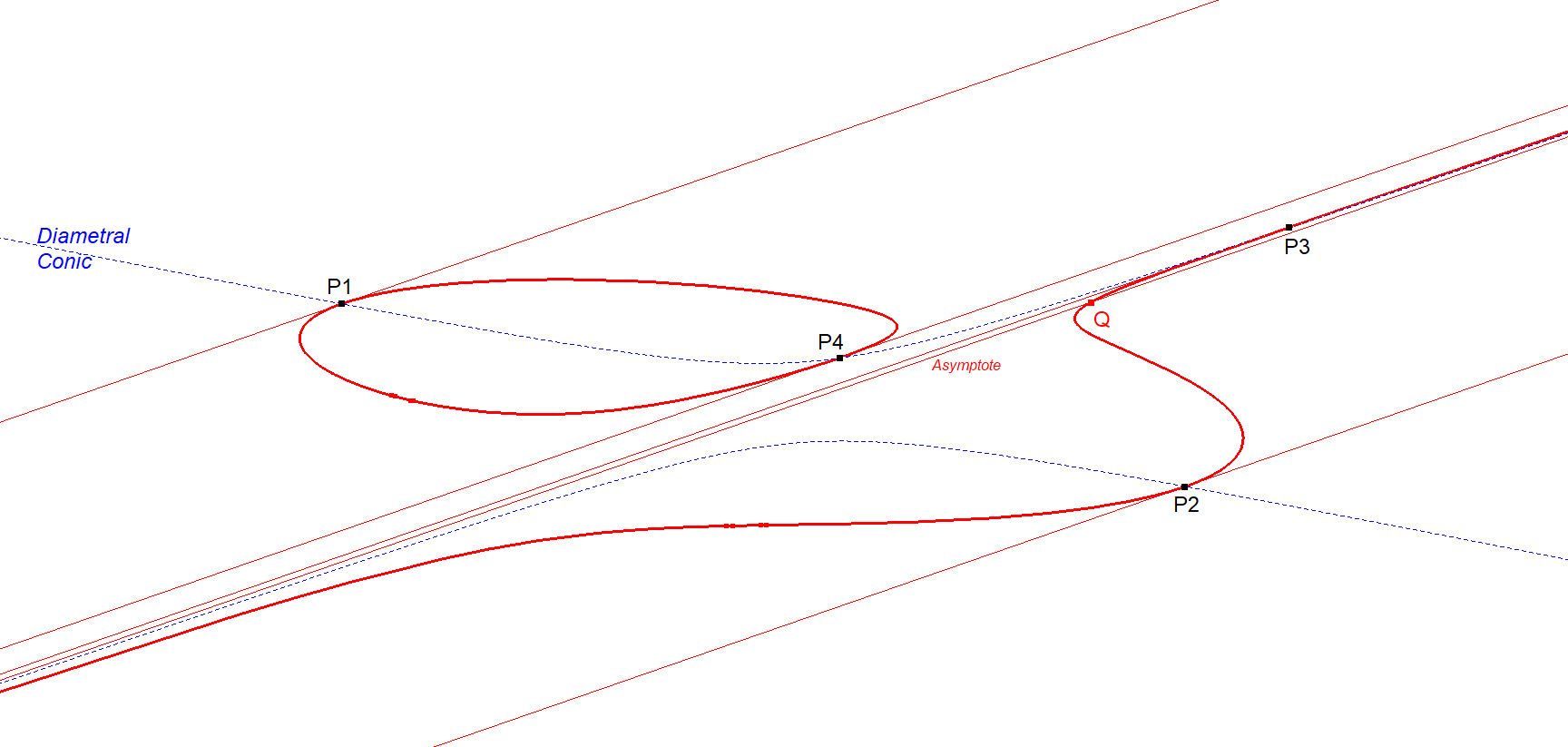
CU2-Bipartite Cubic-20-Anallagmatic Points.fig

Picture Anallagmatic Points on a Tripartite Cubic

Here there are 3 real asymptotes and 3×2 real Anallagmatic Points.

Note: There are also Tripartite Cubics generating sets of 4 real Anallagmatic Points.

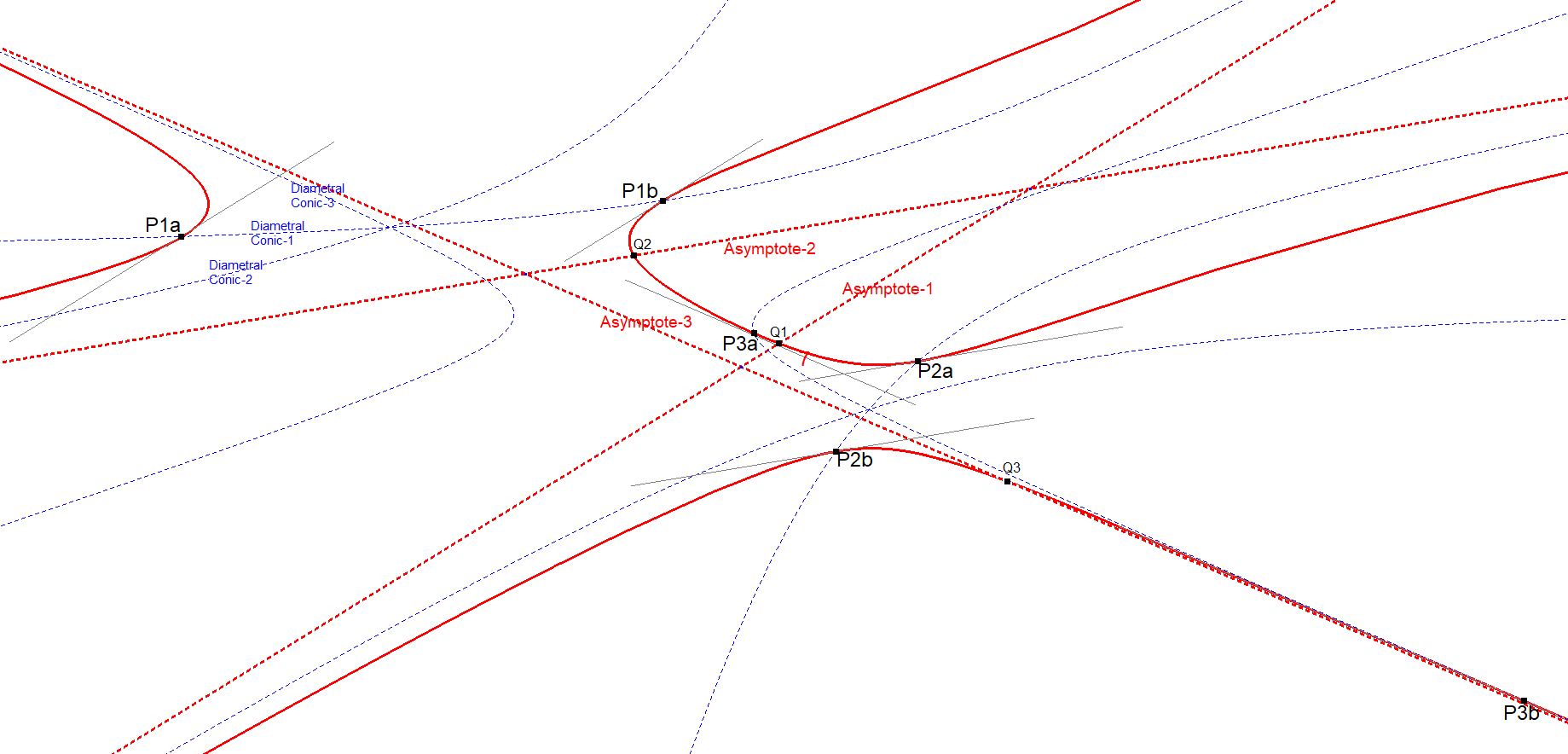
CU3-Tripartite Cubic-41-DiametralConics-Anall-Points.fig

Properties

• Each set of 4 Anallagmatic Points forms a Quadrangle whose vertices of the Diagonal Triangle also lie on the cube. This triangle is called the Quasi-Miquel triangle (CU-IP-3P1).
• Each vertex of this Quasi-Miquel Triangle (CU-IP-3P1) is the center of a Quasi-Moebius Transformation (CU-IP-3Tf1).
• Tangents at the Anallagmatic Points enclose strips/segments within which the cubic ‘moves’. This can easily be seen in the images above.

Estimated human page views: 6