CU-IP-P2 CU-Asy-Crosspoint
Each cubic CU has at least one real asymptote that intersects the CU itself at a fixed point, referred to here as the CU-Asy-Crosspoint.
The other two asymptotes may be real or imaginary, each with its own CU-Asy-Crosspoint.
CU-Asy-Crosspoints can be either finite or infinite.
General Construction
- In this construction we have 2 reference points P1, P2 on CU and we know the direction of the asymptote.
- Draw points -P1 and -P2 as intersection points of the asymptote-parallels through P1 and P2.
- Draw point -P1-P2 as the 3rd intersection point of P1.P2 with CUc.
- Draw point +P1+P2 as the 3rd intersection point of -P1.-P2 with CUc.
- Now the 3rd intersection point of the line through the points -P1-P2 and +P1+P2 is CU-IP-P2.
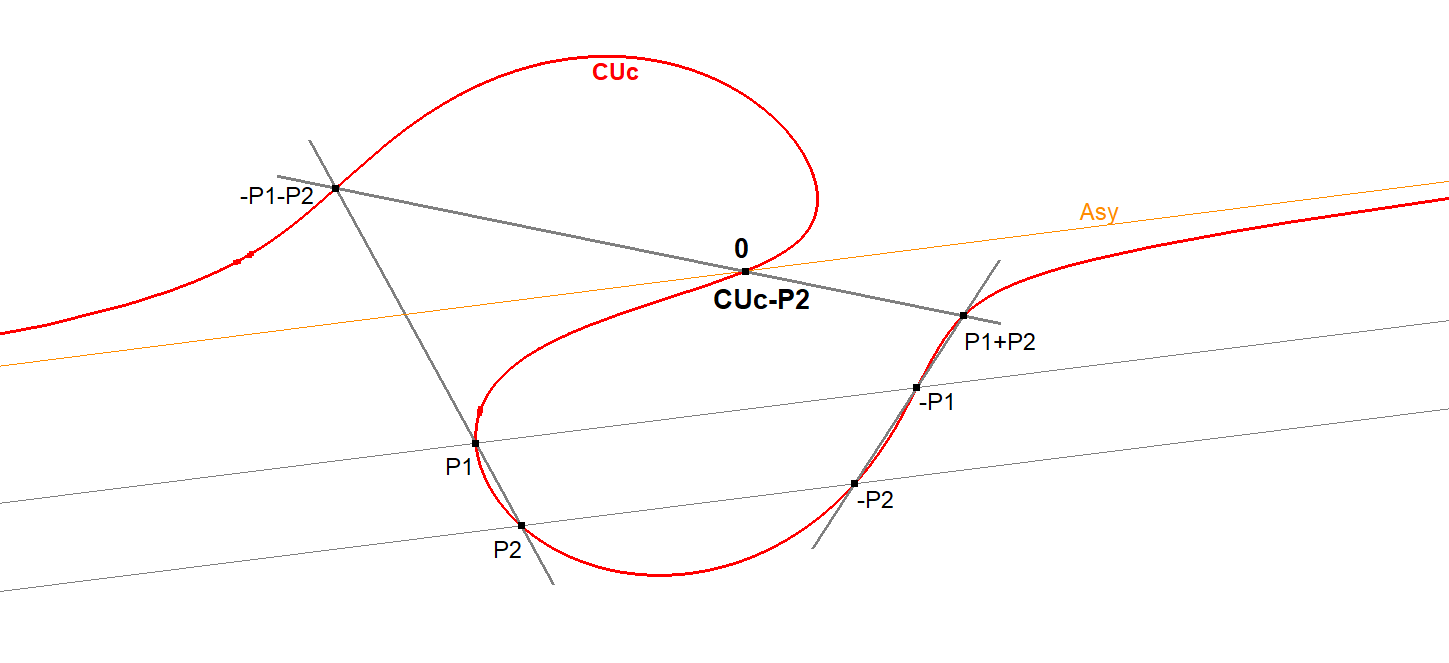
CUc-P2 CUc-Asy-Crosspoint-10-simple construction.fig
CU Point Validation
- Let IP be the Infinity Point of the asymptote.
- P1 + Q1 + IP = N; P2 + Q2 + IP = N;
- P1 + P2 + P3 = N;
- Q1 + Q2 + Q3 = N;
- X + P3 + Q3 = N –> X = N – P3 – Q3 = N – (N – P1 – P2) – (N – Q1 – Q2) = N – (N – P1 – Q1) – (N – P2 – Q2) = N – IP – IP = N – 2IP.
Therefore X = N – 2IP –> X + 2IP = N, which has the same value as the intersection point of CU and the Asymptote.
Construction-1 on a Circular Cubic
In this construction we have 3 reference points P1,P2,P3 on CU.
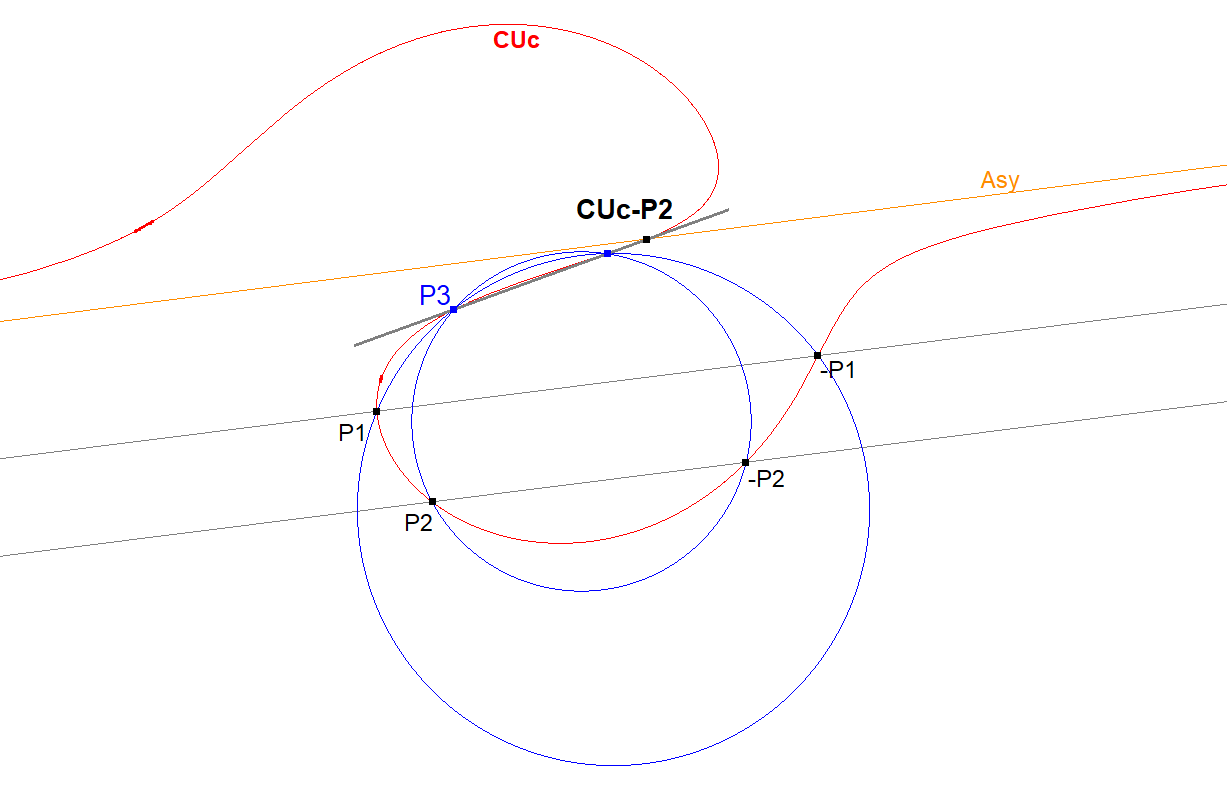
CUc-P2 CUc-Asy-Crosspoint-20-simple construction.fig
CU Point Validation
Construction-2 on a Circular Cubic
In this construction we have 7 reference points on CUc.
CUc-P2 = 3rd intersection point CUc_7P-P1.CUc_7P-P2 (in EPG 7P-s-P2.7P-s-P4)
In this method the direction of the asymptote is not used.
See QPG#787
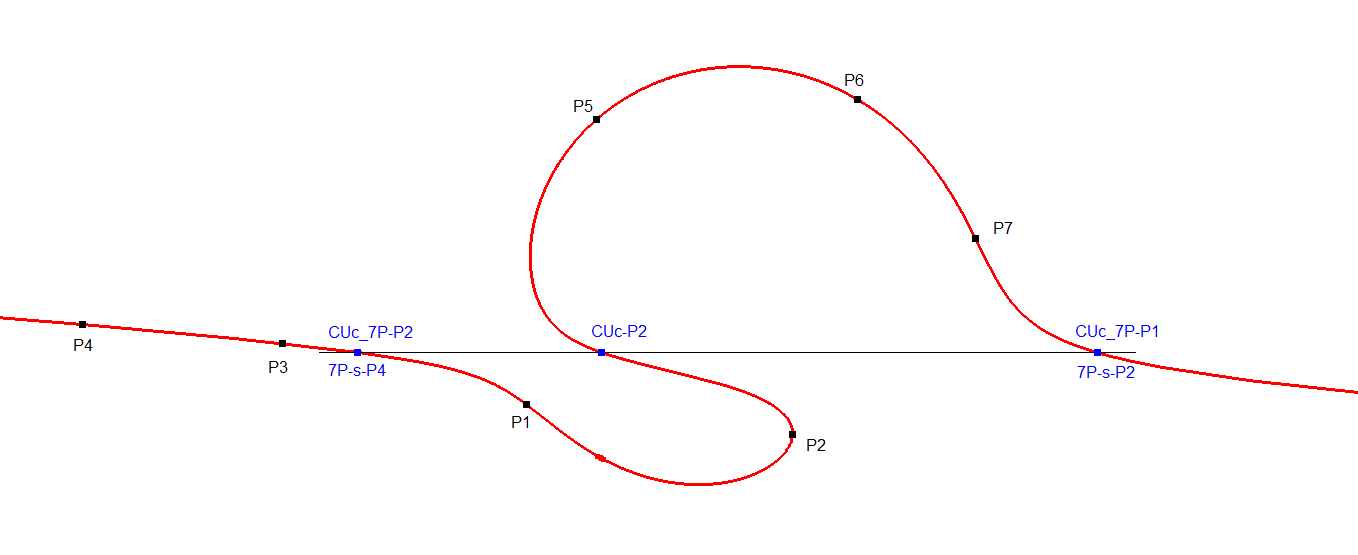
7P-s-P5 Intersection point 7P-Cubic and its Asymptote-00.fig
CUc-P2 CUc-Asy-Crosspoint-30-construction.fig
CU Point Validation
Properties
Estimated human page views: 45
