CU-IP-Tf1 Set of 3 IP-Involutary Conjugates

On a general cubic CU we have 3 asymptotes, of which at least one will be real.

We can draw lines parallel to these asymptotes denoted as Asy-parallel lines.

In the projective plane an Asy-parallel line will always pass through the infinity point (IP) of the related asymptote, which also is an infinity point of the general cubic. Therefore any asy-parallel line will have no more than 2 real intersection points with CU. When it passes through a given real CU-point, there will be just one other real intersection point of the Asy-parallel line with CU. This point is called here the P-Asy-parallel Point.

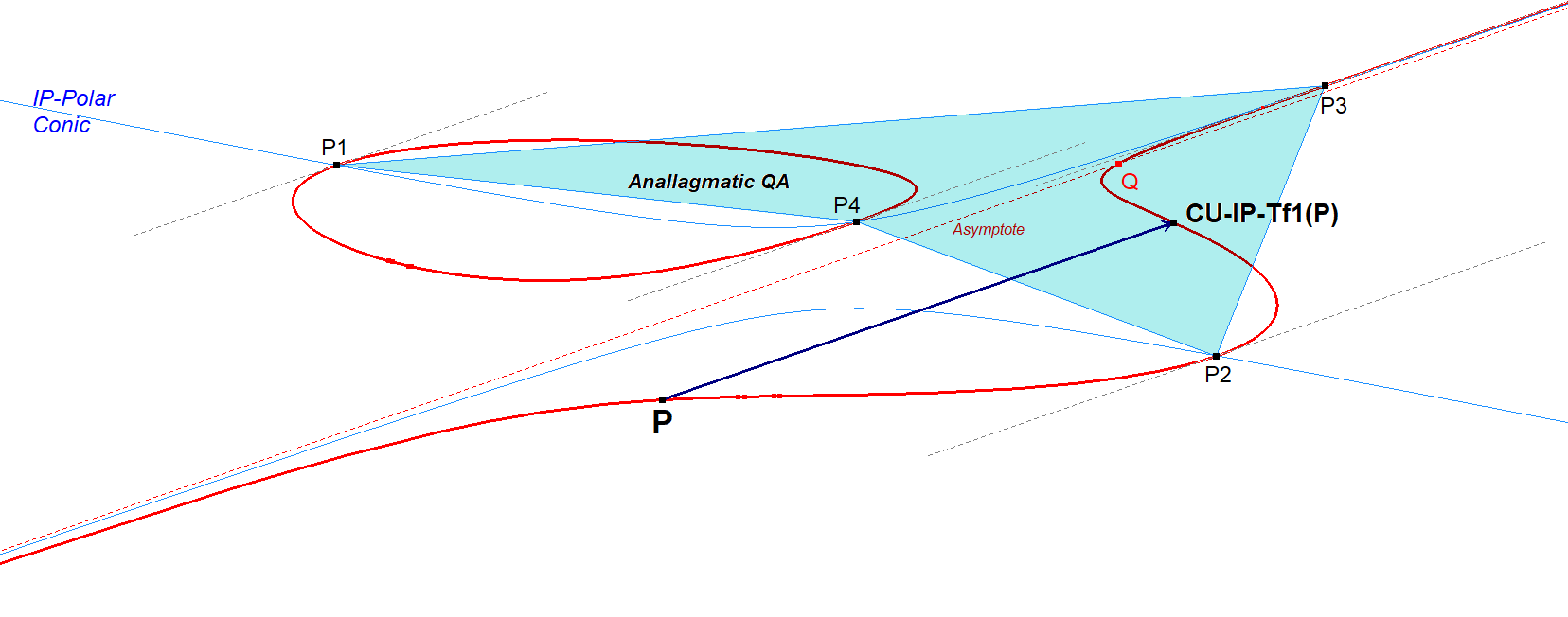
On a general cubic we have 4 points where Asy-parallel lines touch the cubic, the so-called Anallagmatic Points (CU-IP-4P1). They are the intersection points of CU and the IP-Polar Conic (CU-IP-Co1) related to the infinity point IP of the related asymptote. These 4 points form a Quadrangle QA. For each such QA exists an Involutary Conjugate (see QA-Tf2 in EQF) mapping any point on CU to another point on CU.

The special thing about this Involutary Conjugate is that it maps a point P on CU to its P-Asy-parallel Point. See also QPG#2055.

Estimated human page views: 7