CO-Tf2 Conical Pole
The Conical Pole P of a line L wrt some conic CO is the intersection point of the tangents to CO at the intersection points of CO with L. In this construction P is called the pole and L is called the polar.
This construction is very intuitive. However there is a flaw in the definition because the pole cannot be constructed under all circumstances. For example when CO is some ellipse and L is not intersecting the ellipse, then the construction fails.
Therefore another construction is made that includes the result of the first construction:
The pole of some line L wrt some conic (see CO-Tf1) is the intersection point of the polars of two random points from line L.
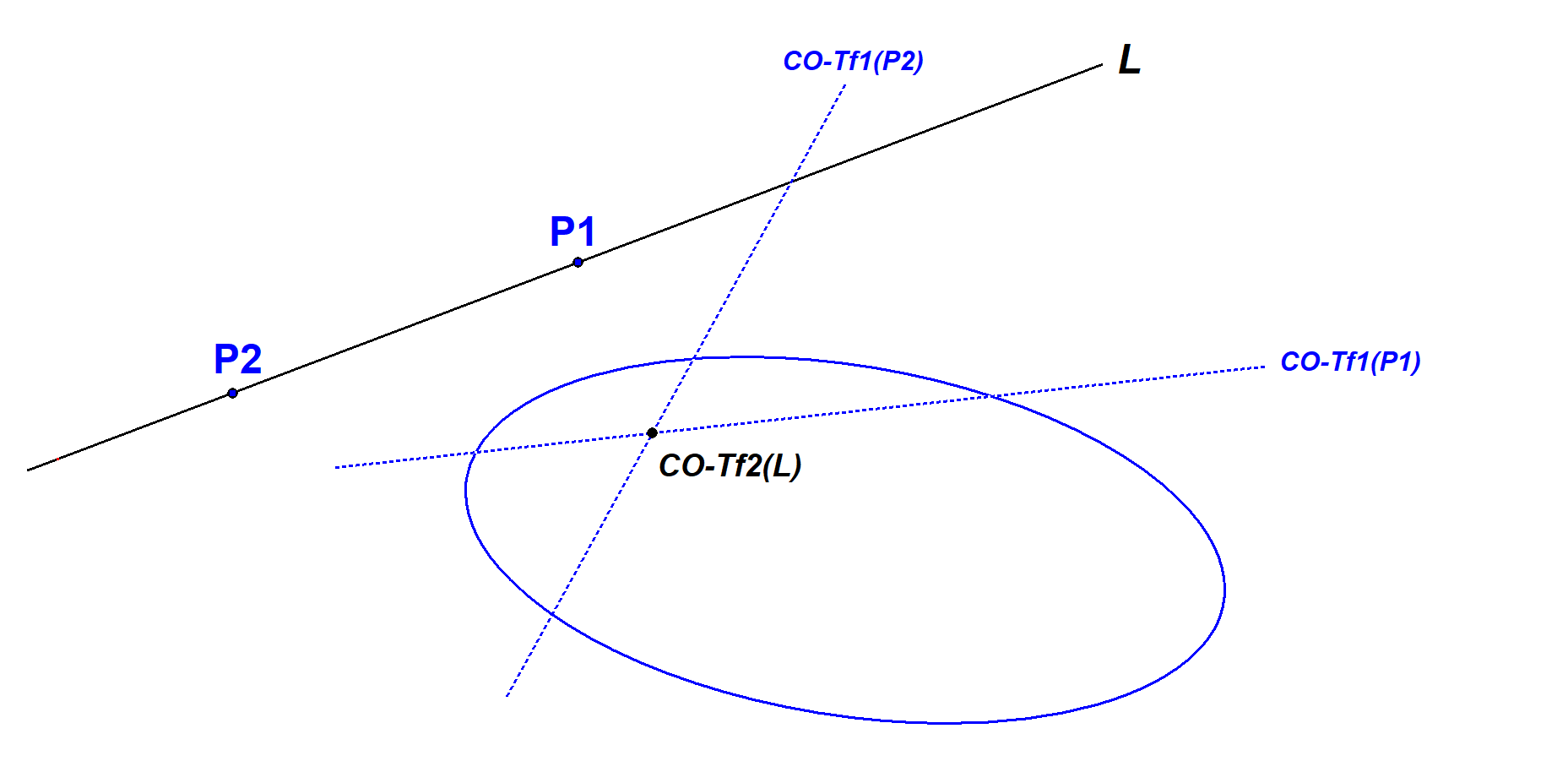
Another construction
This construction is from Eckart Schmidt. See Ref-34, QFG#2811.
- Let L be the line to be transformed.
- Let Pl be the pole (Co-Tf2) of L.
- Let Lp be the line through Pl perpendicular to L.
- Let Lc be the reflection of P.Co-P1 in the main axis of Co.
- Then Co-Tf4(L) is the polar of the intersection point of Lp and Lc.
Estimated human page views: 291
