CO-Tf5 Rectangular Selfpolar Triangle

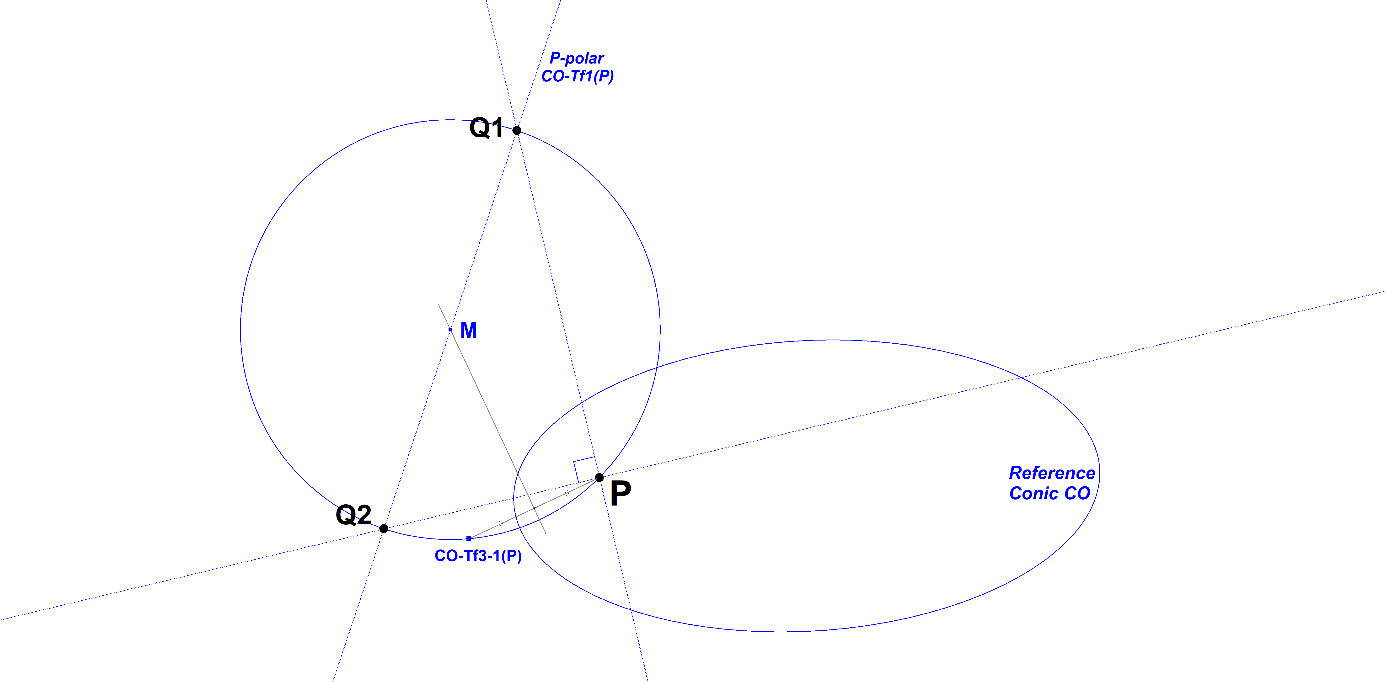
Let CO be the Reference Conic and P be a random point.

There are two points Q1 and Q2 on the polar of P wrt CO, such that triangle P.Q1.Q2 is a rectangular selfpolar triangle wrt CO,

meaning that:

• Q1.Q2 is the polar of P wrt CO,
• P.Q1 is the polar of Q2 wrt CO,
• P.Q2 is the polar of Q1 wrt CO,
• P.Q1 _|_ P.Q2.

The rectangular selfpolar triangle P.Q1.Q2 can be constructed as follows:

1. Construct CO-Tf3^-1(P), the inverse of the Scimemi Transformation CO-Tf3 of P wrt CO.
2. This point lies on the circumcircle of P.Q1.Q2.
3. Let M be the intersection point of the P-polar CO-Tf(P) and the perpendicular bisector of P.CO-Tf3^-1(P)).
4. Q1 and Q2 are the intersection points of the P-polar and the circle centered in M through P.

Properties

• Let 5P be a 5-Point and P a random point. Construct in each of the 5 Component Quadrangles of the 5P the 4P-Cubic(P). The 4P-Cubic(P) is constructed conform QA-Cu7, only with a variable pivot P instead of the fixed pivot QA-P4. Apart from P, there will be 2 points Q1 and Q2 through which all Cubics pass. P, Q1, Q2 form the Rectangular Selfpolar Triangle of P wrt the 5P-circumscribed conic. See [34], QFG#3445, #3640, #3641, # 3642.

Estimated human page views: 4