nG-1

nG-1 Notes on the n-Gon

Definition and Importance of Order

An n-Gon is a geometric figure composed of n points cyclically connected by n line segments, forming a bounded shape. Unlike general configurations of n points or n lines—where the order of elements is irrelevant—n-Gons rely heavily on the order of reference points and lines. This ordered structure is essential in defining specific points, lines, and curves associated with the n-Gon.

From Unordered Sets to Ordered Cycles

When working with an n-Point or n-Line configuration (where order does not matter), we can derive multiple ordered sets of points or lines. These ordered sets can be used to construct n-Gons, just as unordered sets of points can be used to form triangles.

In essence, every n-Point or n-Line configuration contains a certain number of n-Gons, determined by the number of cyclic permutations of the elements— where reverse orders are considered equivalent to the original.

Combinatorics in Geometry

This is where combinatorics intersects with the geometry of poly-figures. The number of distinct n-Gons that can be formed from an n-Point or n-Line configuration is given by the formula:

(n − 1)! / 2

This formula accounts for cyclic permutations while eliminating duplicates caused by reversed orderings.

Examples of n-Gon Counts

Configuration	Formula	Number of n-Gons	Name
4-Point	(4−1)! / 2 = 3	3	Quadrigons
5-Point	(5−1)! / 2 = 12	12	Pentagons
6-Point	(6−1)! / 2 = 60	60	Hexagons

Summary of Bounded Figures

The number of 4-Gons (bounded figures) in a 4-Point is 3:

The number of 5-Gons (bounded figures) in a 5-Point is 12:

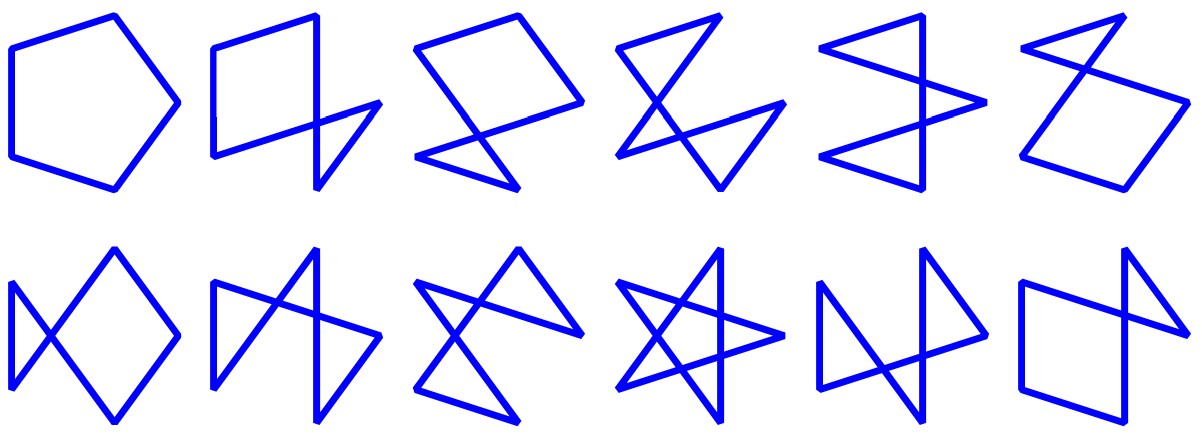
The number of 6-Gons (bounded figures) in a 6-Point is 60:

etc.