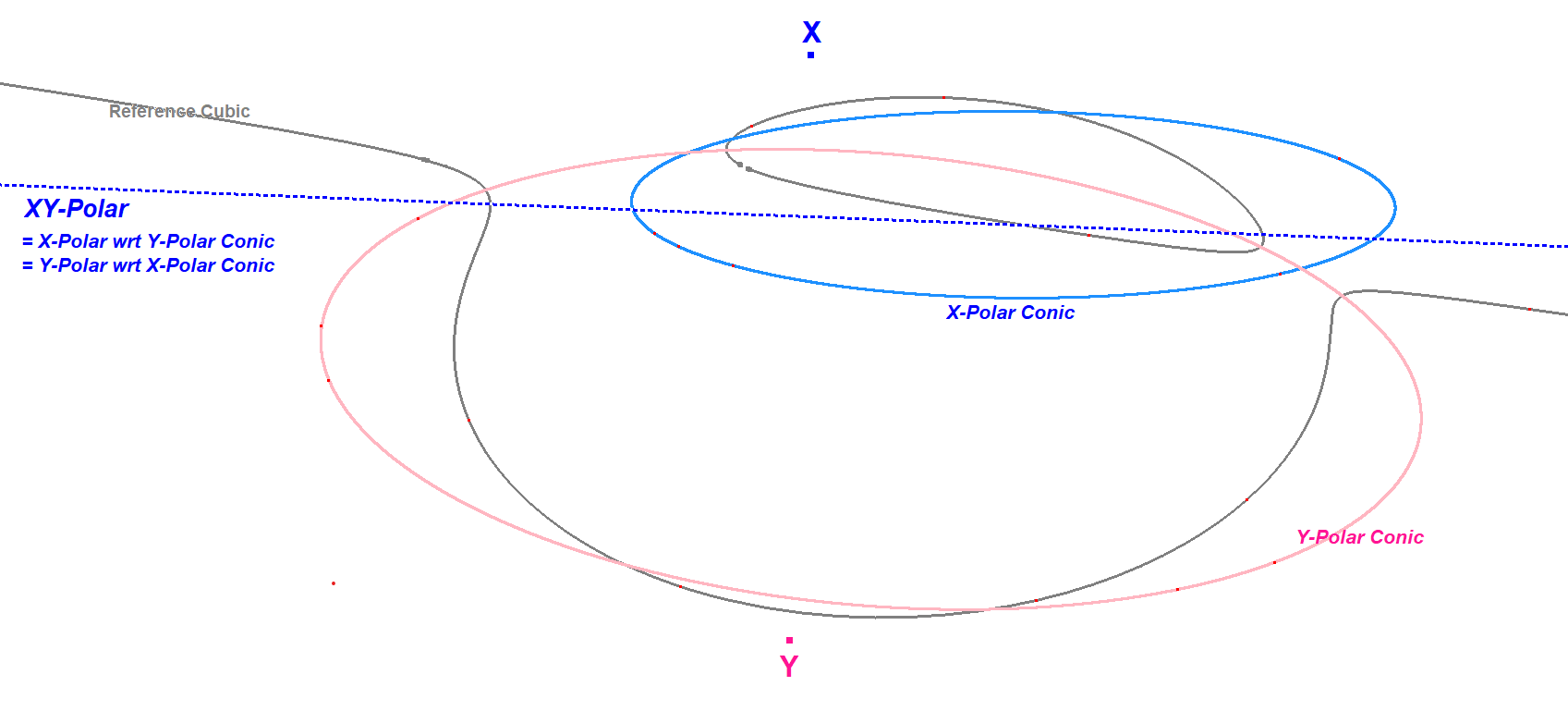
CU-2P-L2 Mixed XY-Polar
Given a general Cubic CU and two random points X and Y on the cubic, then:
- the X-Polar of the Y-Polar Conic = the Y-Polar of the X-Polar Conic.
This Polar is called the Mixed Polar or XY-Polar or Mixed XY-Polar.
A description of the P-Polar Conic can be found at CU-P-Co1. It is the conic through P (not necessary on CU) and the 4 points of tangency from the tangents at P to CU.
The P-Polar is just the polar of some point P wrt some conic.
Properties
- It isn’t maybe easy to construct the Polar Line of an infinity point IP wrt an X-Polar Conic. This now easily can be constructed as the X-Polar Line wrt the IP-Polar Conic. And the IP-Polar Conic we know, it is the Diametral Conic CU-IP-Co1.
- Given 2 points (X,Y) on a line L1 and another point Z on a 2nd line L2. The locus of the intersection point of the Mixed YZ-Polar and the Mixed XZ-Polar with variable Z on L2 is a conic called the Poloconica CU-2L-Co1. Every point Z on this conic has the property that given any 2 points (X,Y) on L1 or L2 and another random point Z on the not used line of (L1,L2) the XY-Polar, YZ-Polar and the XZ-Polar will concur in one point.
- [J. de Vries, On polar figures with respect to a plane cubic curve] (see [81]) describes these items:
- 1. Given a general Cubic CU and two random points X and Y not necessary on the cubic, then the X-Polar of the Y-Polar Conic = the Y-Polar of the X-Polar Conic. This the XY-Polar Lxy.
- 2. Theorem: The locus of points Z for which Lxy, Lyz, Lxz concur is a conic he called Poloconica.
Estimated human page views: 63
