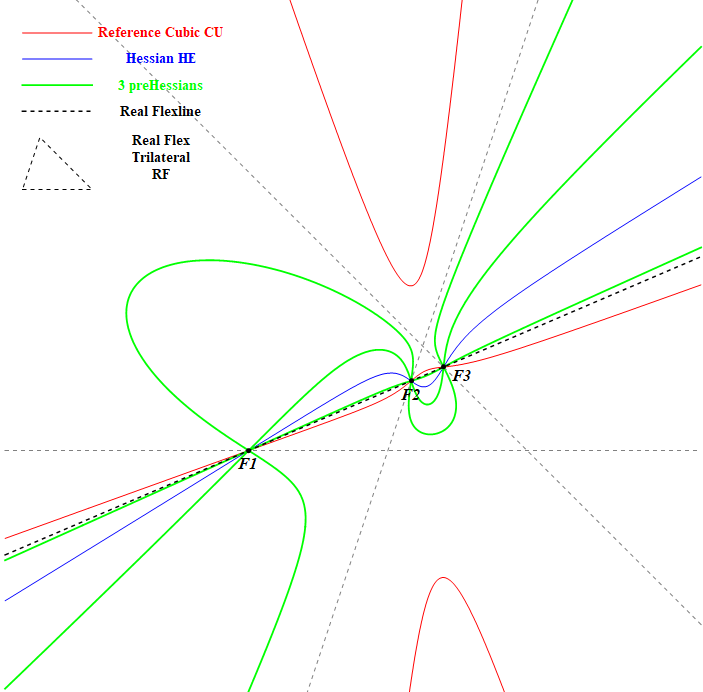
CU-3Cu1  The three PreHessians of CU

Since a Hessian is also a cubic, it is also possible to calculate the Hessian of the Hessian, and further downwards.

Moreover it is possible, knowing some cubic CU, to find out for which upper cubic CU is the Hessian. There are 3 of these cubics called the PreHessians pHE₁, pHE₂, pHE₃.

So per definition the Hessian of all three cubics pHE₁, pHE₂, pHE₃ will be CU.

So “upwards” there are 3 PreHessians of a cubic and “downwards” there is 1 Hessian per cubic.

For a formal description of the construction of the three PreHessians see [16b].

Actual calculation of the prehessians

• Let the Reference Cubic be of the form (Hesse’s Form) CU = FE + k a₁ a₂ a₃ RF, where FE = a₁³ x³ + a₂³ y³ + a₃³ z³ and RF = x y z .
• Then a preHessian should be of the form pHEt = FE + t a₁ a₂ a₃ RF
• The calculated Hessian of preHessian pHEt will be 3 a₁³ t² x³ + 3 a₂³ t² y³ + 3 a₃³ t² z³ – a₁ a₂ a₃ (108 + t³) x y z and should be CU = a₁³ x³ + a₂³ y³ + a₃³ z³ + a₁ a₂ a₃ k x y z
• They are identical when 3 a1³ t² / a1³ = – a₁ a₂ a₃ (108 + t³) / (a₁ a₂ a₃ k)
• That is the case for t = t1, t2, t3, with
  • t1 = -k + k²/W + W
  • t2 = -k – ((1 + i √3) k²)/(2 W) + 1/2 i (i + √3) W
  • t3 = -k + (i (i + √3) k²)/(2 W) – 1/2 (1 + i √3) W

• where W = (-54 – k³ + 6√3(√(27 + k³))^1/3

• As can be seen the roots are independent of (a₁, a₂, a₃) and only depend on k.
• It appears that:
  • t1 is real when k < -3
  • t2 is real for all k
  • t3 is real when k < -3

CU-HE-pHE-01.nb

Estimated human page views: 8