CU-5P-P1 6^th intersection point of a 5P-conic

Given five random points P1, …, P5 on reference cubic CU.

According to Bezout’s theorem any conic (curve of 2^nd degree) has six intersection points with a cubic (curve of 3^rd degree) in the projective complex plane. These intersection points of a conic can be real or imaginary as well as finite or infinite.

Consequently, when we have 5 points P1, …, P5, there will be a 6^th intersection point of the conic through P1, …, P5 with CU.

The existence of this point is obvious, but its construction is not that simple.

CU-5P-P1 6th Intersection Point with 5P-Conic-01.fig

Construction

• We use for the construction these cubic properties:
• When 2 cubics intersect in 8 points, then they will intersect in a fixed 9^th point, that will be the 9^th intersection point for all cubics through these 8 points. This is called the 8P-Cayley Bacharach Point CU-8P-P1. Denote CB=Cayley-Bacharach Point. See CU-8P-P1 for its construction.
• Given 7 points on a reference cubic CU. Then for every point Pi there will be a Cayley-Bacharach Point CBi(P1,…,P7,Pi) with special property that 3^rd intersection point P.CBi with CU will be fixed for every general location of Pi. This point is called CU-7P-P1, the 7P-Pivot Point. See CU-7P-P1 for its construction.
• When 2 cubics intersect in 9 points and 3 are collinear then the other 6 will be coconic.
• When 2 cubics intersect in 9 points and 6 are coconic then the other 3 will be collinear.

Now we can proceed to the actual construction of the 6^th intersection point of conic (P3,P4,P5,P6,P7) with CU.

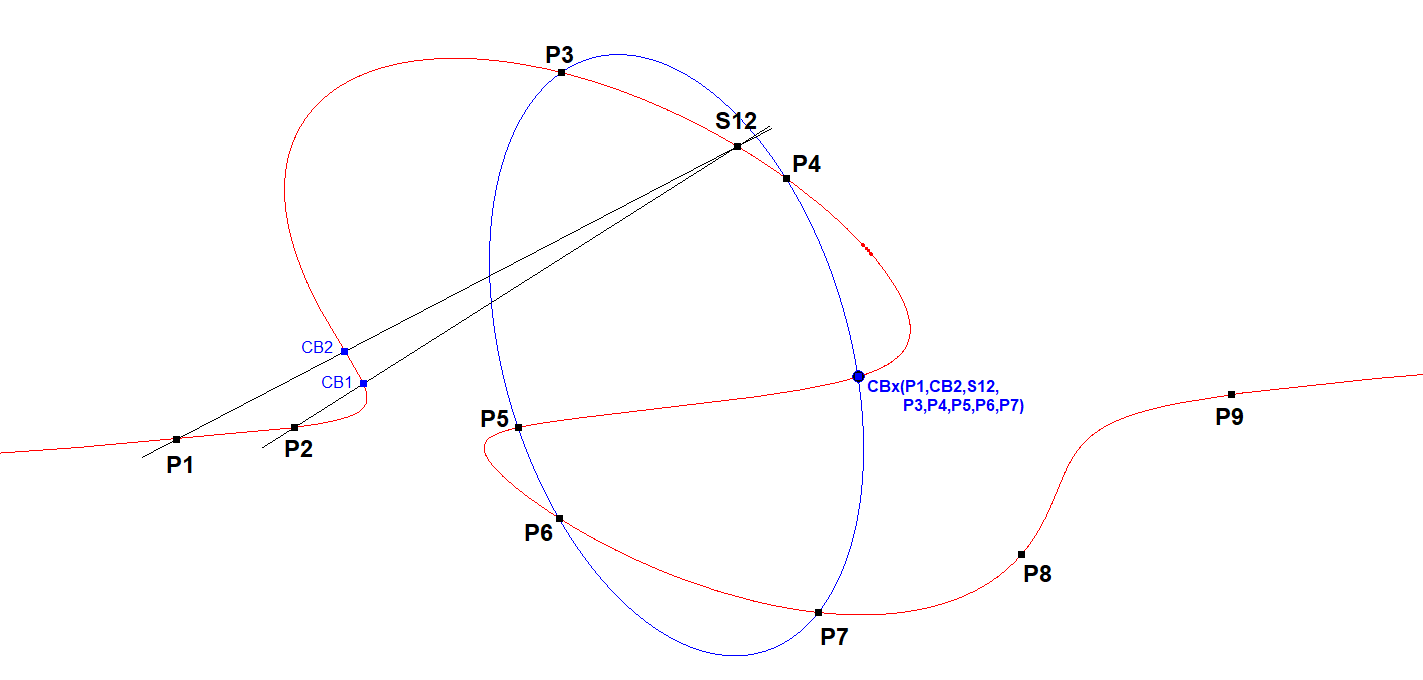
• Determine 9 points P1, …, P9 on the cubic.
• Construct CB1=CB(P2,P3, …, P9) and CB2=CB(P1,P3, …, P9).
• Lines P1.CB2 and P2.CB1 will meet in 7P-Pivot Point S12 on CU.
• Construct CBx=CB(P1,CB2,S12,P3,P4,P5,P6,P7). The first three points are collinear, therefore CBx will be the 6^th intersection point of conic(P3,P4,P5,P6,P7).

Estimated human page views: 2