← Previous Next →

CU-9L1 Harmonic Polars

Let P be a point on the cubic curve CU.

Draw three lines (Lp1,Lp2,Lp3) through P, each intersecting the reference cubic in two additional points. This yields six points: (P1a,P1b), (P2a,P2b), (P3a,P3b).

According to Schröter (see [82], page 242) these six points are coconic when P is a flexpoint. The form of the conic will be different for each set of (Lp1,Lp2,Lp3). However the Harmonic Polar of P wrt all these different conics will be a fixed line.

These polars are called the Harmonic Polar of Fi (Fi being one of the 9 Flexpoints CU-9P1).

Other names are “Polar Axis of a flexpoint” or “Flexpolar”.

See also QPG#2046, #2050, #2054.

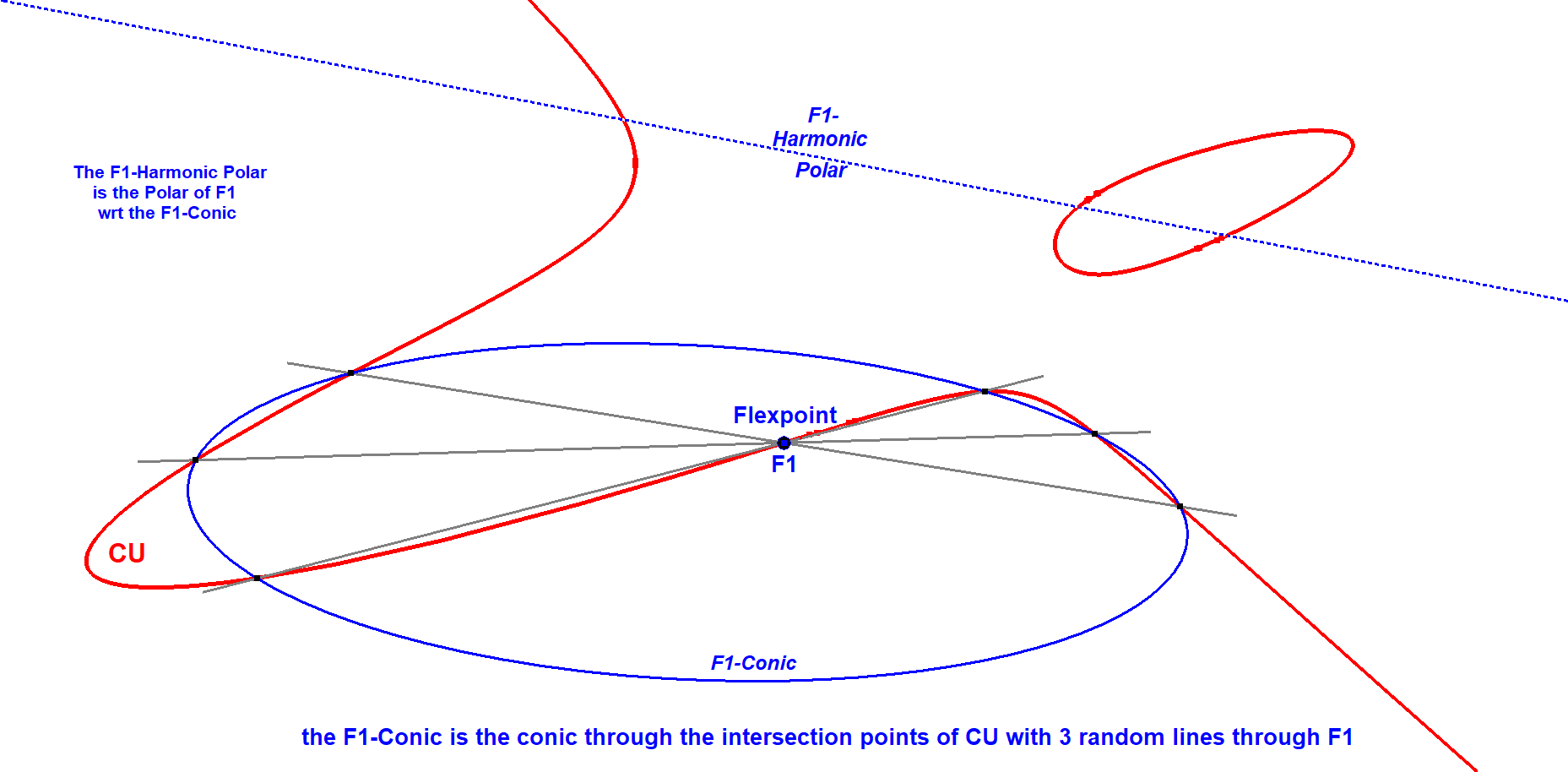
Infovisual CU-9L1-infovisual-cvt-01.png

CU-9L1 Fi-Harmonic Polars-10.fig

The 3 Harmonic Polars of the 3 real Flexpoints F1, F2 and F3 concur in a fixed point.

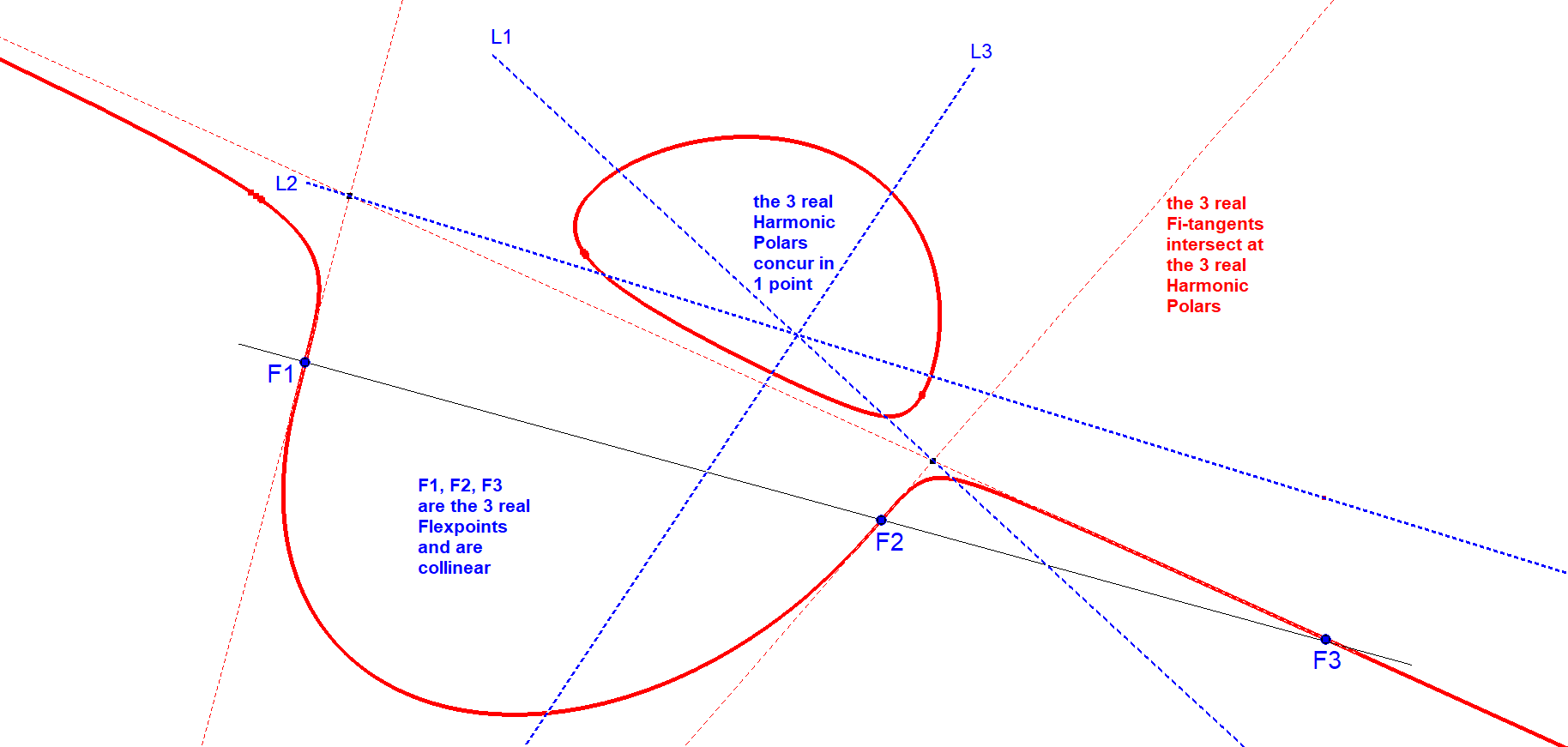
Infovisual CU-9L1-infovisual-cvt-02.png

CU-9L1 Fi-Harmonic Polars-21.fig

Since there are 9 Flexpoints (3 of them real and 6 imaginary) there also will be 9 Harmonic Polars (3 of them real and 6 imaginary).

Properties
  • The polar conic of a flexpoint Fi wrt CU is a conic degenerated in two lines: the Fi-Harmonic Polar and the CU-Fi-Tangent.
  • The three CU-Fi-Tangents form a triangle with its vertices on the three real Fi-Harmonic Polars.
  • The three real CU-Fi-Flexlines (see CU-12L1) form a triangle with its vertices on the three real Fi-Harmonic Polars.
  • The Harmonic Polars L1, L2, L3 intersect CU each in 3 points forming 3 triangles, per triangle with their sides through resp. F1, F2, F3. These triangles are mutually perspective, all with the common intersection point of (L1,L2,L3) as perspector and the line through (F1,F2,F3) as perspectrix.
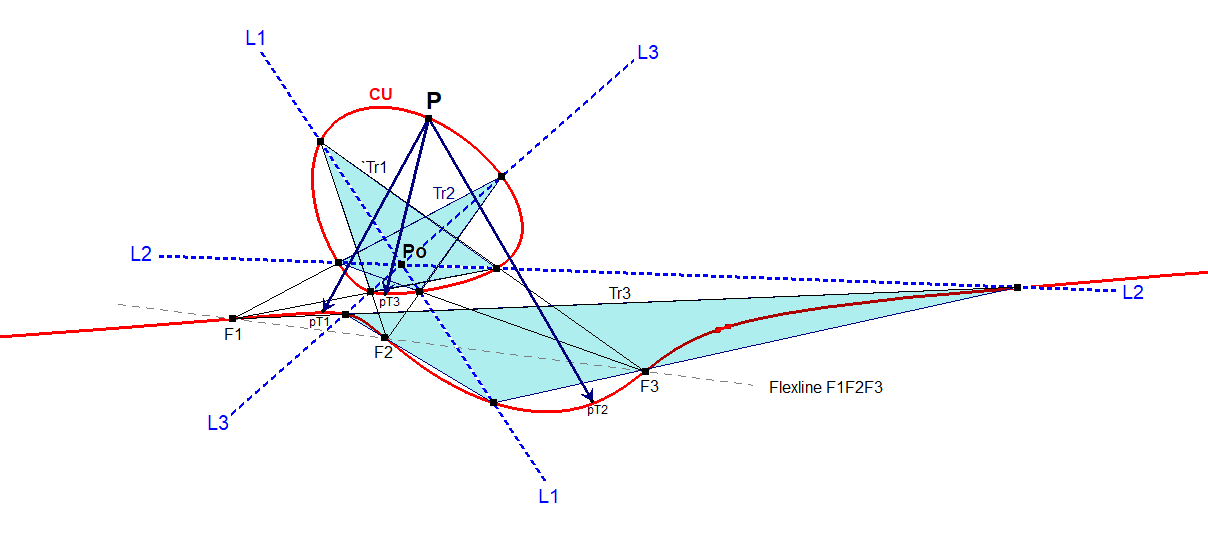
Infovisual CU-9L1-infovisual-cvt-03.png

CU-Cu1 Hessian-112a-Pi-Isoconjugates.fig

  • CU is a non-pivotal Isocubic wrt each of these triangles and with fixpoint the common intersection point Po of (L1,L2,L3). The product of the isoconjugates of some cubic-point P wrt the 3 triangles is the identity, where the isoconjugate is QA-Tf2 with QA=(Po+vertices of anticevian triangle of reference triangle). See QPG#2380,#2381,#2386-#2388,#2390.


Estimated human page views: 8

Scroll naar boven