CU-IP-Co2 Central Conic or QF-Conic
There are three Central Conics, each associated with one of the asymptotes (infinity points) of the cubic. When two asymptotes of a given cubic are not real, their corresponding Central Conics are also not real.
The construction of a Central Conic is straightforward. Given a reference cubic CU, let Asy1 be one of its asymptotes, corresponding to Infinity Point IP1, and intersecting CU at Q1. Draw a pencil of lines through Q1, each intersecting CU at two additional points, Si and Ti. Let Mi be the midpoint of Si and Ti. The locus of Mi forms the Central Conic of CU associated with IP1.
For the first description of the QF-Conic/Central Conic, see QPG#2045.
To indicate that the conic belongs to a specific cubic CU and an infinity point IP1, it can be referred to as the CU-IP1-Central Conic or simply the IP1-Central Conic.
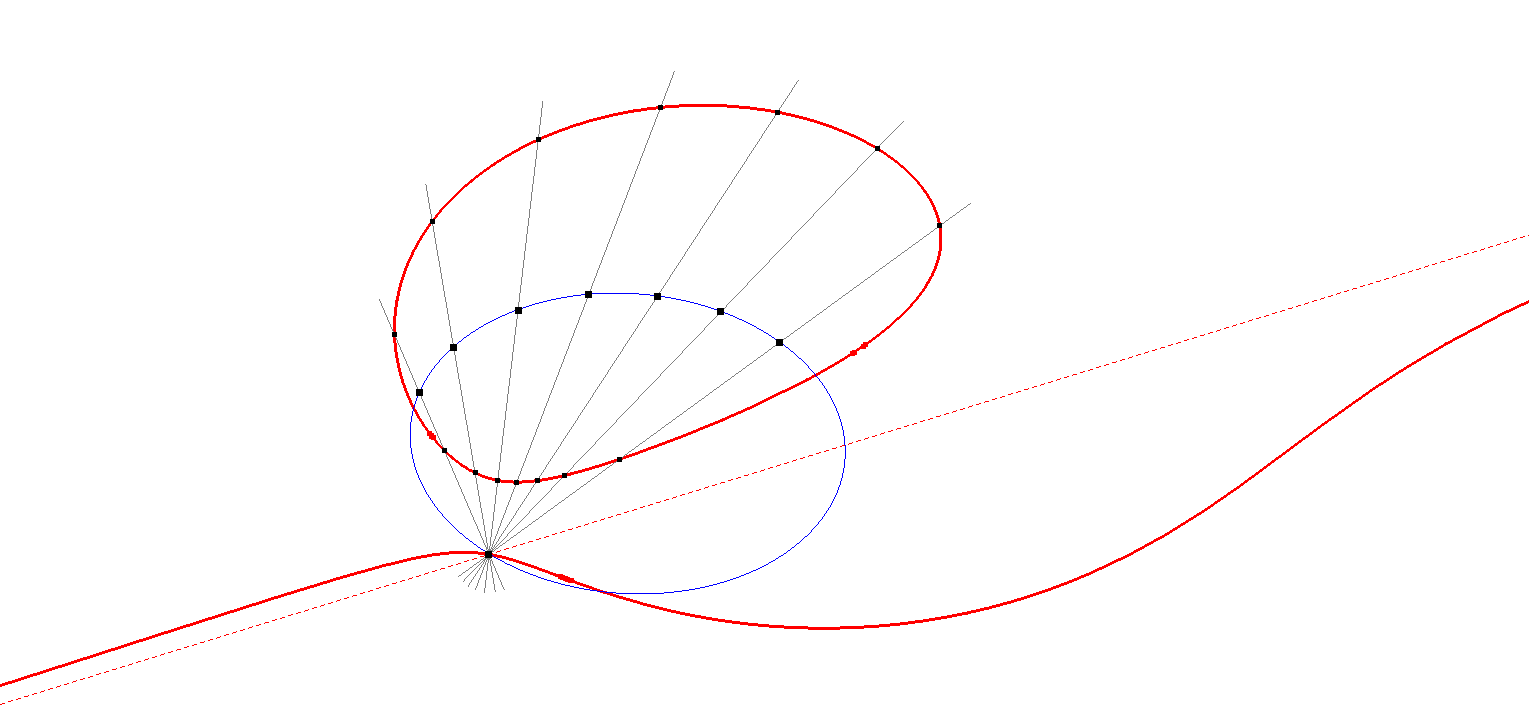
CU-IP-Co2 IP-Central Conic-01.fig
The IP-Central Conic serves as a mold for the shape of the cubic and as a similarity model for other auxiliary conics related to the cubic (see CU-IP-3Tf1 and CU-9P-P1/P2/P3).
Its shape can be either an ellipse or a hyperbola. It forms an ellipse when the other two infinity points are imaginary, and a hyperbola when they are real. This occurs because these two infinity points lie on the conic itself, meaning that IP2 and IP3 belong to the IP1-Central Conic. Note that (IP1, IP2, IP3) can be cyclically interchanged.
Construction of the Second and Third CU-Asymptotes
The IP1-Central Conic contains the infinity points IP2 and IP3.
Therefore, when IP1, IP2, and IP3 are real points and the IP1-asymptote is known, the IP2- and IP3-asymptotes can be constructed as follows:
- Construct the IP1-Central Conic Co1 as described above.
- Determine its Co1-asymptotes, which will be parallel to the CU-asymptotes associated with the infinity points IP2 and IP3.
- Construct the CU-asymptotes Asy-2 and Asy-3 using the general construction method outlined in CU-IP-P2.
Special Property
The Polar Conic of a vertex of the Asy-Triangle contains the same infinity points as the two asymptotes passing through this vertex. Consequently, it also shares these infinity points with the corresponding Central Conic/QF-Conic. This follows from the definition that a P-polar conic passes through the P-points of tangency, which, in the case of a point on a CU-asymptote, are the CU-infinity points.
QF-Circle/Central Circle at a Circular Cubic
The IP-Central Conic is a circle in the case of a Circular Cubic CUc.
A QF-Conic of a General Cubic is derived from the QF-circle in a circular cubic CUc.
There is only one real QF-Conic/-Circle because a Circular Cubic has only one real asymptote.
This circle contains several familiar CU-points viz
- Point Q, the CU-Asy Crosspoint CU-3P2a
- Point F, the Singular Focus of a Circular Cubic, which is the intersection point of the tangents at the circular points at infinity, which actually are the two imaginary asymptotes of CUc, which makes it the intersection point of CU-IP-L1b and CU-IP-L1c.
- Points M1a,M1b,M1c, being the 3 Quasi-Miquel Points (vertices of CU-IP-3P1a), of which 1 or 3 are real points.
Apart from these properties the QF-Circle is the locus of midpoints (S1,S2), being the 2nd and 3rd intersection points of a pencil of lines through Q.
QF-Conic/Central Conic at a General Cubic CU
This QF-Circle also does exist for the General Cubic, but in this case it is a conic with these properties:
- It is a conic instead of a circle.
- There are 3 of them, for each CU-asymptote there will be one QF-Conic, but sometimes 2 of them (CU-IP-L1b and CU-IP-L1c) will be imaginary.
- The CU-Asy Crosspoint CU-3P2a lies on QF-conic CU-IP-Co2a (the a-version of the conic).
- The Asy-Asy-Crosspoint CU-IP-Q1a (being CU-IP-L1b^CU-IP-L1c) lies on the a-version of the QF-conic. This point will be the point opposite of CU-3P2a on the QF-Conic.
- The infinity points of the not involved asymptotes CU-IP-L1b an CU-IP-L1c also lie on the a-version of the QF-conic. When they are real points the QF-Conic will be a hyperbola, when they are imaginary then the QF-Conic will be an ellipse.
- Points M1a,M1b,M1c, being the 3 Quasi-Miquel Points (vertices of CU-IP-3P1a) lie on the a-version of the QF-conic, where 1 or 3 of them will be real points.
- The QF-Conic is the locus of midpoints (S1,S2), where (S1,S2) are the 2nd and 3rd intersection points of a pencil of lines through CU-IP-P2a.
Just like there is an a-version of the QF-conic, there also will be a b-version and a c-version of the QF-conic, cyclologically shifting items.
When the reference cubic has 3 asymptotes without finite CU-Asy Crosspoints Qi, then the QF-Conic will degenerate into two lines, the line-at-infinity as well as the line through CU-IP-3P1a and CU-IP-L1b^CU-IP-L1c.
See introduction and further explanation of this QF-Conic at QPG#2025.
PICTURES
QF-Conic on a Monopartite Cubic:
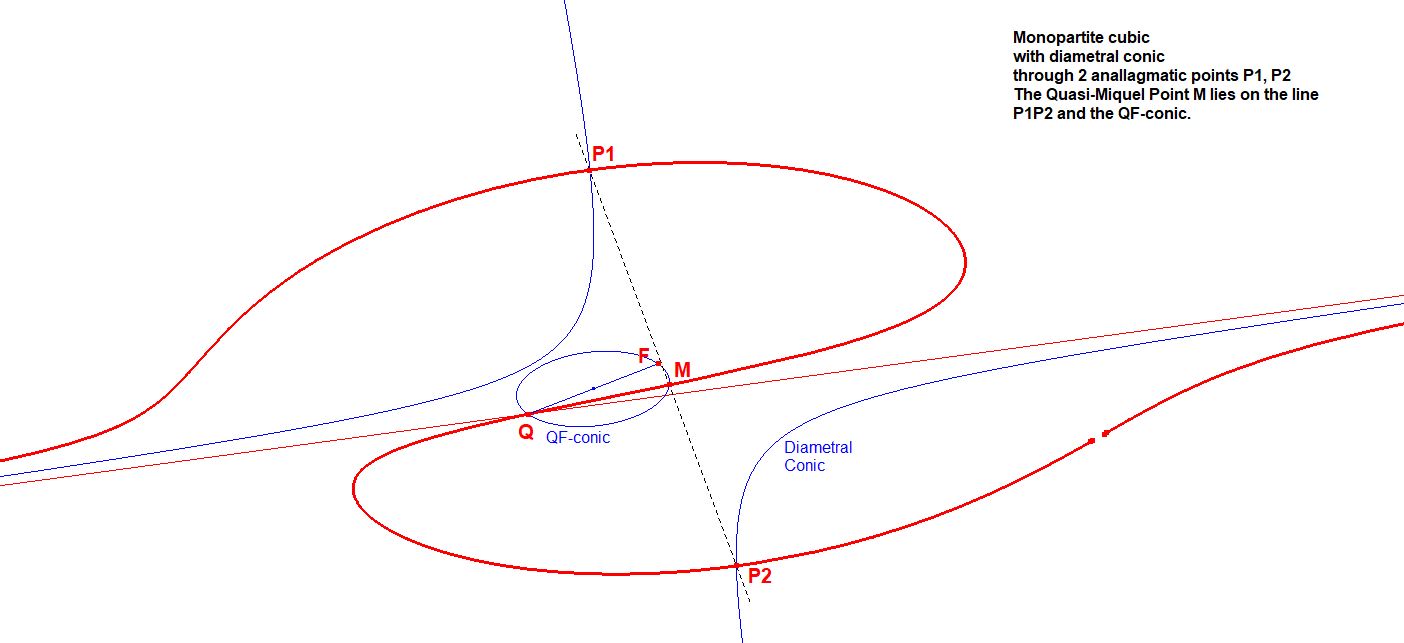
CU1-Monopartite Cubic-02.fig
QF-Conic on a Bipartite Cubic:
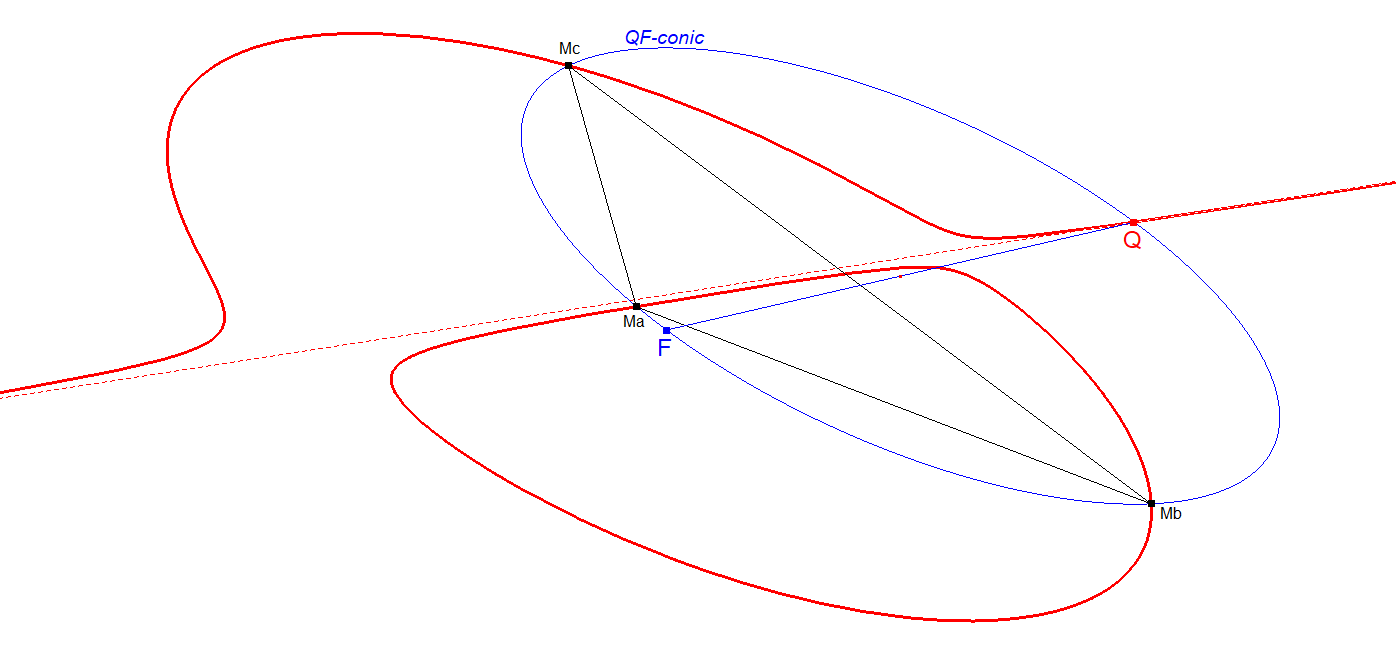
CU2-Bipartite Cubic-10-QF-conic.fig
QF-Conic on a Tripartite Cubic:
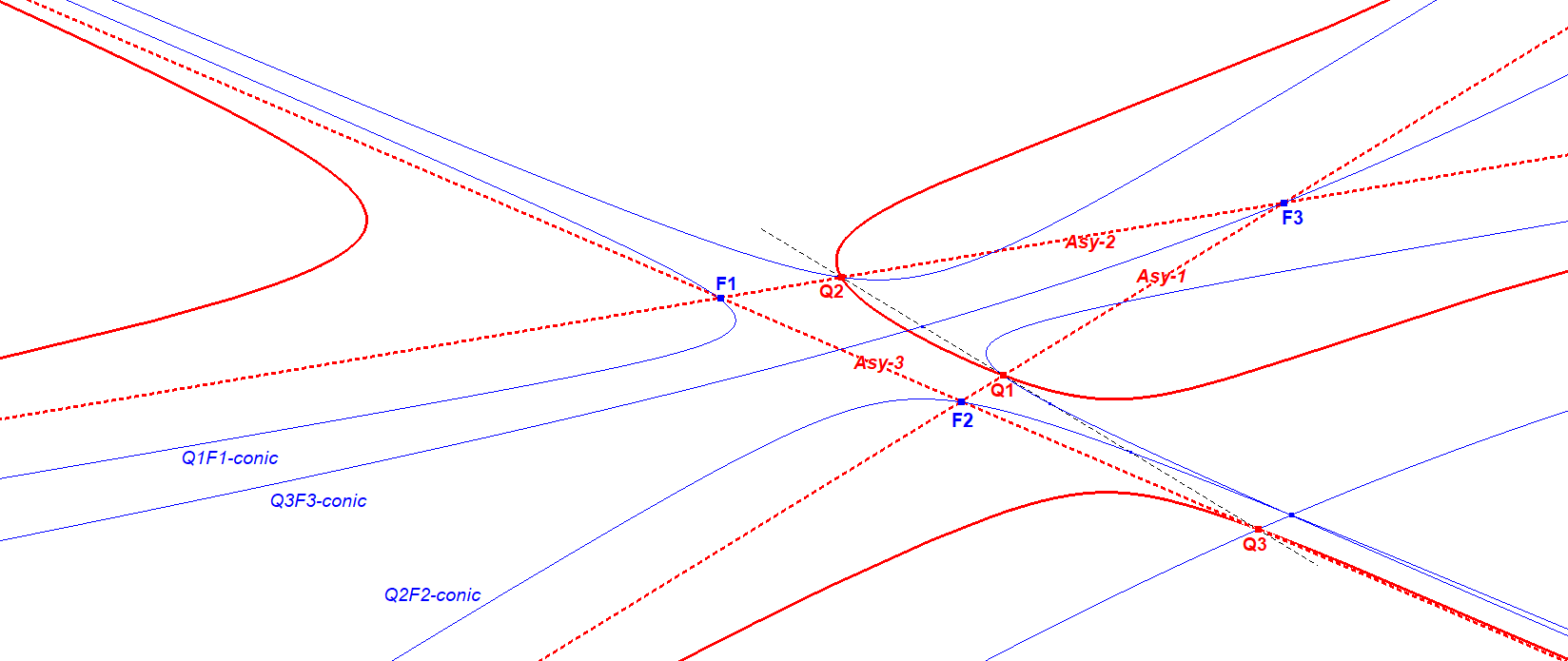
CU3-Tripartite Cubic-10-QF-conic.fig
QF-Conic on a Tripartite Cubic without finite CU-Asy-Crosspoints:
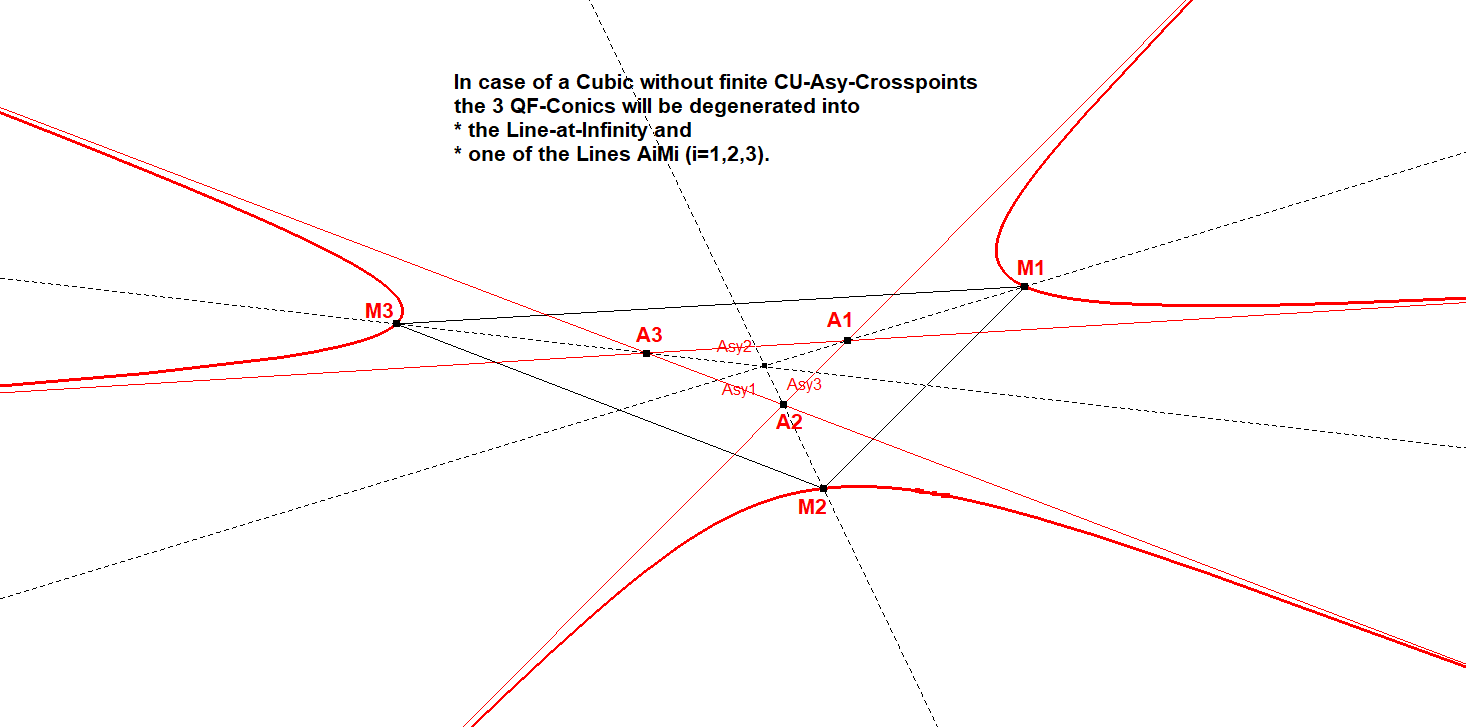
CU3-Tripartite Cubic-2A-2A-2A-02-degenerate QF-Conic.fig
QF-Conic on a Quadripartite Cubic:
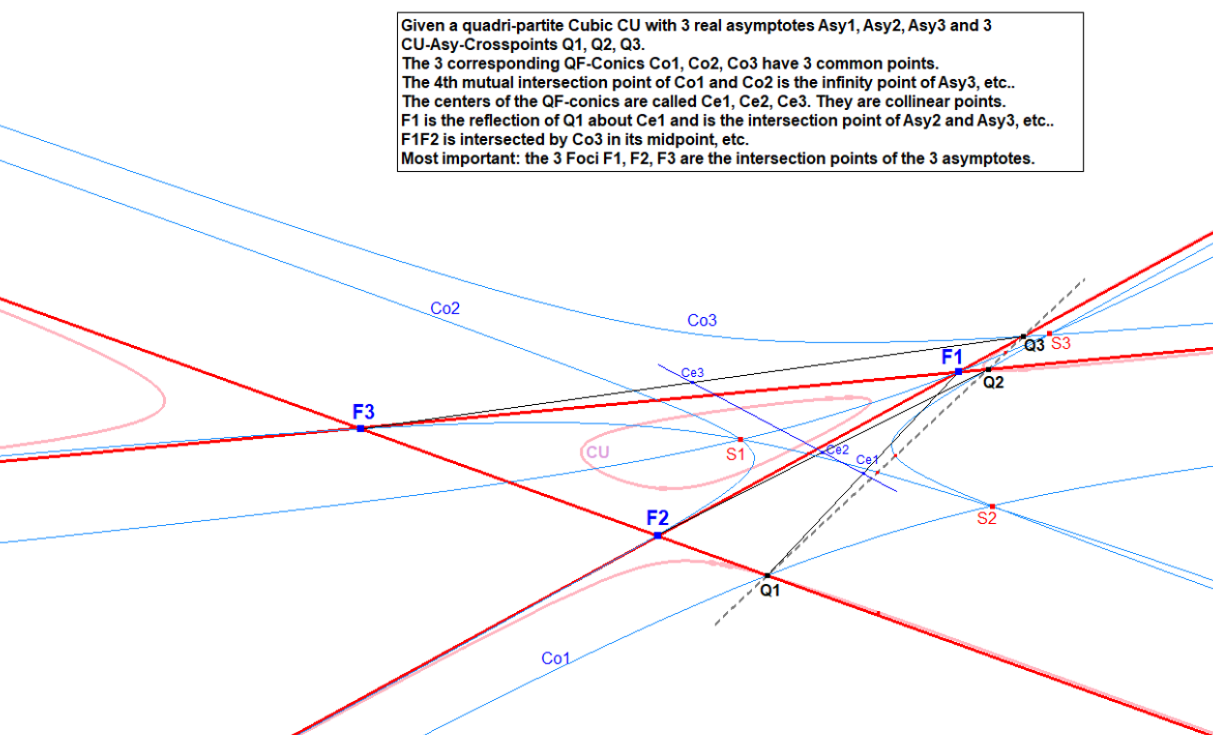
CU4-Quadripartite Cubic-2A-2A-2A-3A-11-Focus Points.fig
Estimated human page views: 67
