CU-L-12P1

Given a line L intersecting reference cubic CU in points P,Q,R.

Draw the Polar Conics (CU-P-Co1) of P, Q and R wrt CU.

The vertices of the 3 PC-intercepted QA's (PC=Polar Conic, QA=Quadrangle) form a Desmic Configuration. See QA-Tr-1.

Every QA is perspective with one of the other QA's in 4 ways, forming the 3rd QA from its perspectors, which makes it a Desmic System.

See QPG#2266.

CU-L-12P1 PQR-PolarConics-DesmicSystem-02.fig

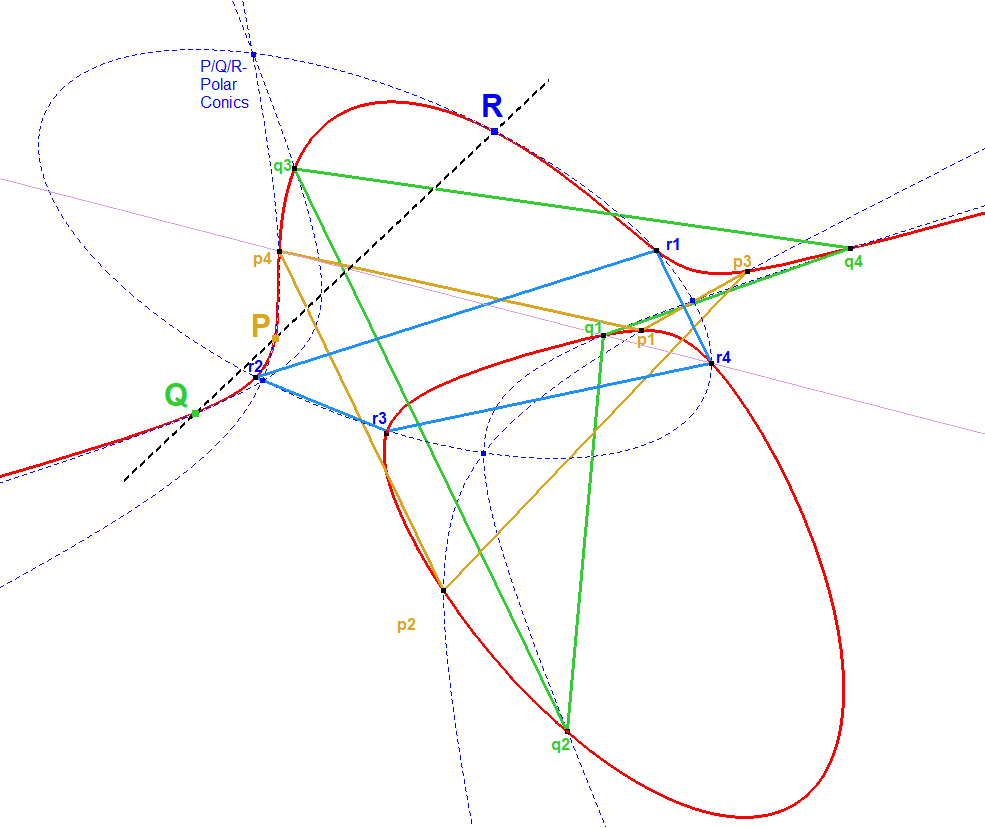
Desmic System made visible

Let p1, p2, p3, p4 be the intersection points of the P-Polar Conic with CU, apart from P.

Let q1, q2, q3, q4 be the intersection points of the Q-Polar Conic with CU, apart from Q.

Let r1, r2, r3, r4 be the intersection points of the R-Polar Conic with CU, apart from R.

In the drawing next collinearities can be checked:

p1-q4-r3, p1-q3-r4, p1-q2-r1, p1-q1-r2

p2-q1-r1, p2-q2-r2, p2-q3-r3, p2-q4-r4

p3-q4-r2, p3-q2-r4, p3-q3-r1, p3-q1-r3

p4-q1-r4, p4-q2-r3, p4-q3-r2, p4-q4-r1.

Which makes it a Desmic System.

Proof of Desmic System using Point-calculation.

Because P and the points of tangency p1, p2, p3, p4 are 'collinear' (points of tangency counted twice),

we know P+2pi=N (i=1,2,3,4) and also Q+2qi=N and R+2ri=N, therefore P+Q+R+2pi+2qi+2ri=3N.(1)

We know P+Q+R=N because P, Q and R are collinear.(2)

Combining (1) and (2) this yields 2pi+2qi+2ri=2N.

This shows that for each version of pi and qi there will be a collinear version of ri (i=1,2,3,4).

Estimated human page views: 5