CU-Q-Co1 Q-Polar Conic of a Cubic

The Polar Conic of some point Q (not on CU) wrt to CU is a conic through the 4 contact points of the tangents from Q to the reference cubic CU.

Two or four of these contact points can be imaginary. In that case these points won’t be visible in the picture, but there will be a conic anyhow and it will only pass through the visible contact points.

Construction

There is a construction method for the P-Polar Conic when P is on CU. See CU-P-Co1.

This method can be used to construct the Q-Polar Conic with Q not on CU.

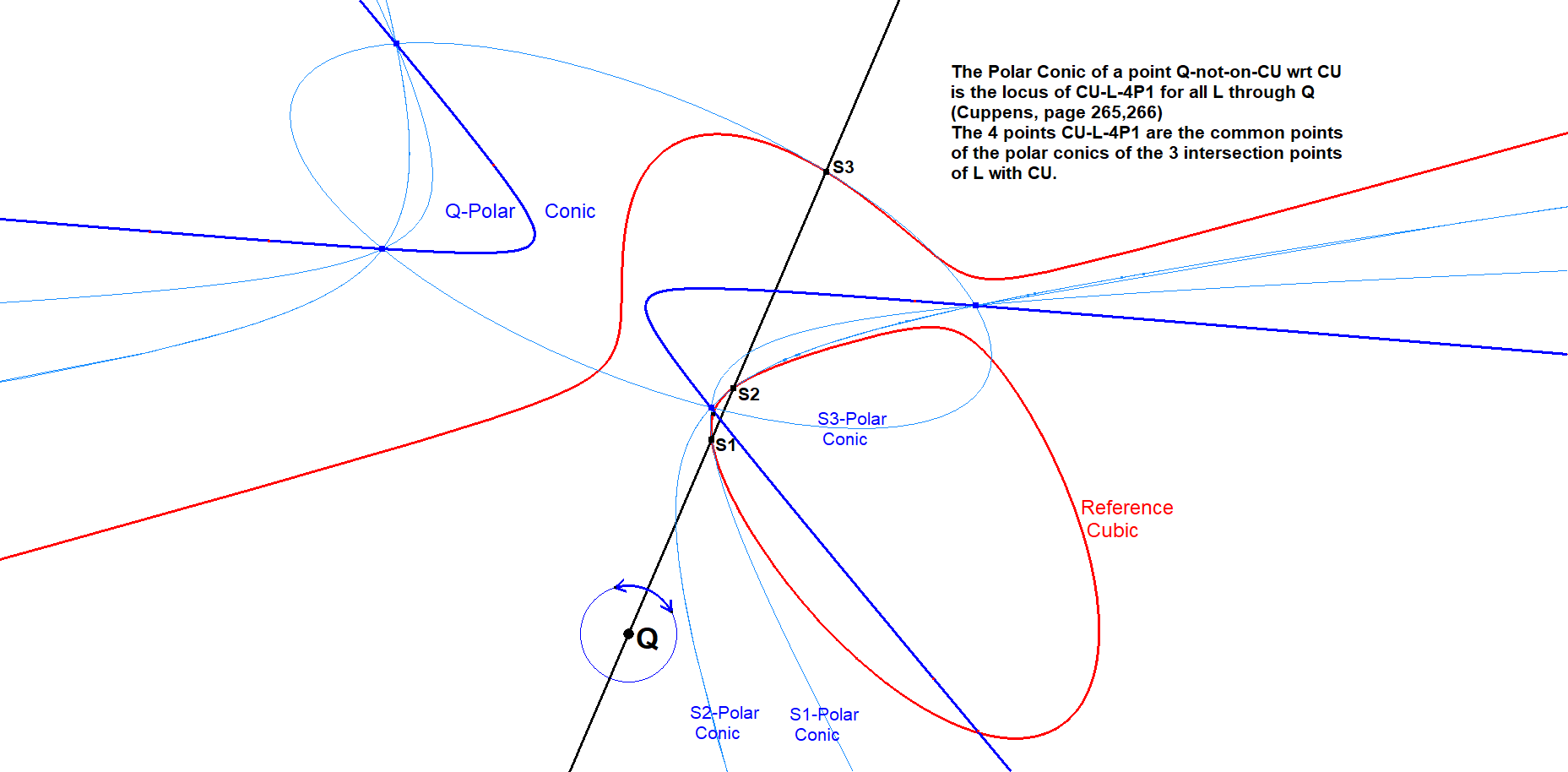
It uses the property that the Polar Conic of a point Q-not-on-CU wrt CU = the locus of CU-L-4P1 for all L through Q (see Cuppens [63], page 265,266). The 4 points CU-L-4P1 are the common points of the polar conics of the 3 intersection points of L with CU.

Estimated human page views: 3