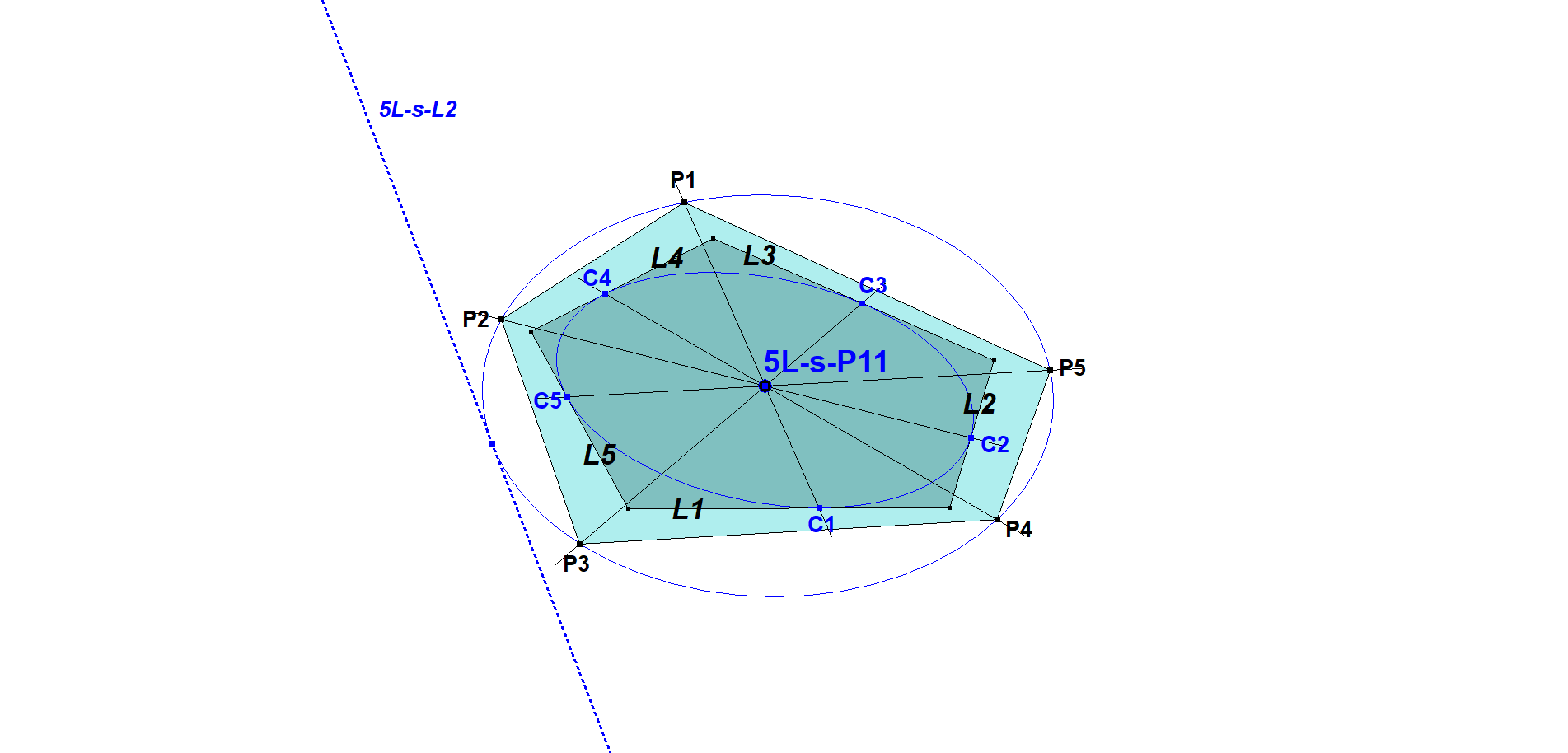
5L-s-P11

5L-s-P11: 5L-Schmidt Point

Given Reference Pentalateral 5L(L1,L2,L3,L4,L5).

Let Pi be QL-Tf10(Li) wrt ref-QL (LjLkLlLm). QL-Tf10 is the equivalent of the Trilinear Pole (also called Tripole) in a Quadrilateral (abbreviated QL or 4L).
Let Ci be the points of tangency of inscribed conic 5L-s-Co1 with resp. L1,L2,L3,L4,L5.
then lines PiCi are concurrent in a new center 5L-s-P11.

Integers i,j,k,l,m each being different numbers from (1,2,3,4,5).

This point was found by Eckart Schmidt. See [66], QPG-messages #359-#362, #365, #367, #368.

The equivalent of 5L-s-P11 in a Pentangle is 5P-s-L1.

Infovisual 5L-s-P11-infovisual-cvt-01.png

Properties

Let Cox be the Circumscribed Conic of (P1,P2,P3,P4,P5). Now line 5L-s-L2 will be tangent to Cox. (mentioned by Bernard Keizer, see [66], QPG-message #360)

Estimated human page views: 160