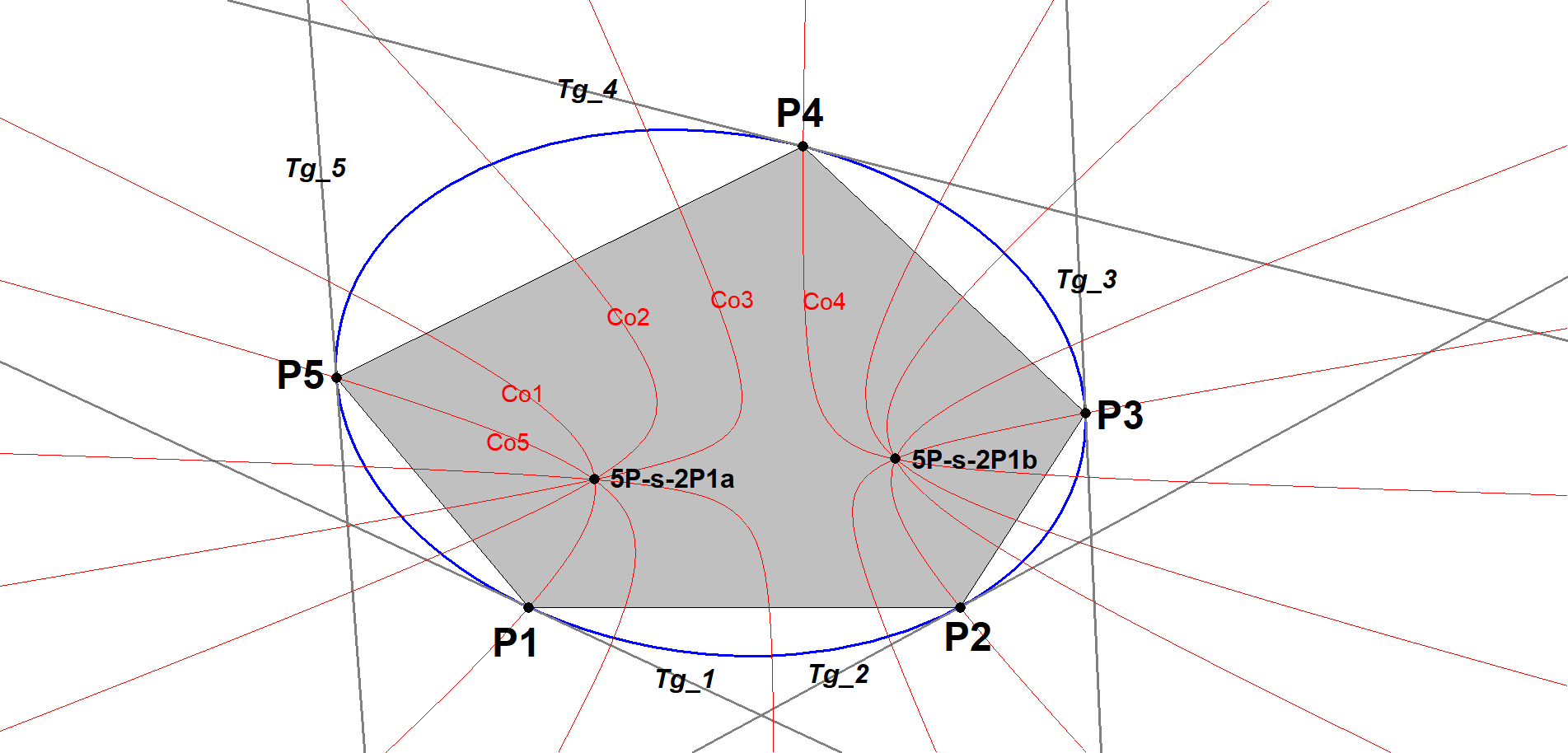
5P-s-2P1 5P-Involutary Double Point
Draw for each Component Quadrangle of the Pentangle the mapped image QA-Tf2 of the line tangent to the circumscribed conic 5P-s-Co1 at the remaining vertex of the Pentangle.
QA-Tf2 (Involutary Conjugate) is a transformation of the 2nd degree and therefore the mapping of all points of a line will be a conic.
The five resulting conics have two common points, which are 5P-s-2P1a and 5P-s-2P1b.
This double point was discovered by Eckart Schmidt. See [34], QFG#2912, #3768.
Properties
- QA-Tf2(Xi) wrt any QA(PiPjPkPl) = (Xi-polar ^ Pm-tangent) wrt 5P-circumscribed-conic.
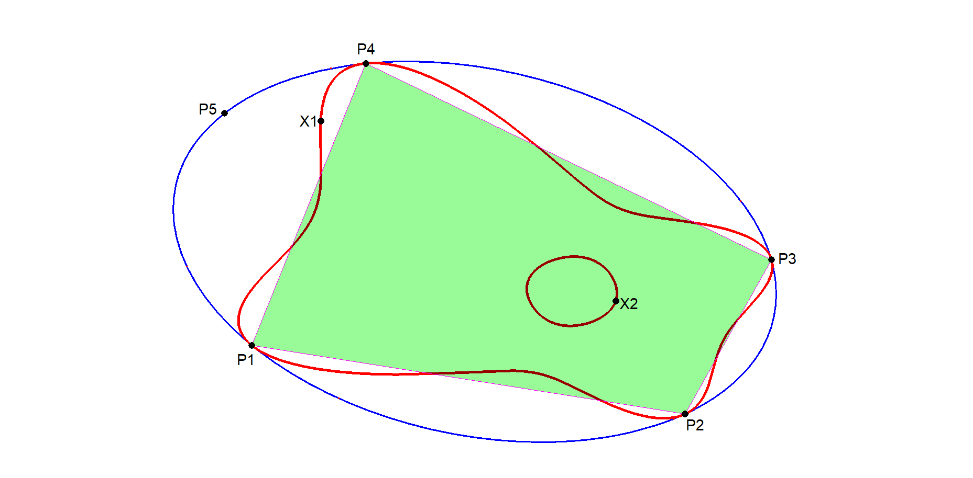
- When the 5P = QA + QA-DT-point Si, then X1 & X2 are the intersection points of the two QA-sides through Si and the QA-DT-side opposite Si.
- Spanning a QA(P1.P2.P3.P4) in a reference Conic CO and some extra point P5 on this conic, the locus of X1 and X2 with fixed QA and variable P5 gives a very special guitar-shaped-locus (see [34], QFG#3772) with these properties:
- It is tangent to CO at the QA-vertices.
- Each of the 6 QA-sides is intersected at the two vertices and two other points, each intersected by one of the defining QA-Tf2(tangent)-conics. Therefore these points can be easily constructed and calculated.
Estimated human page views: 422
