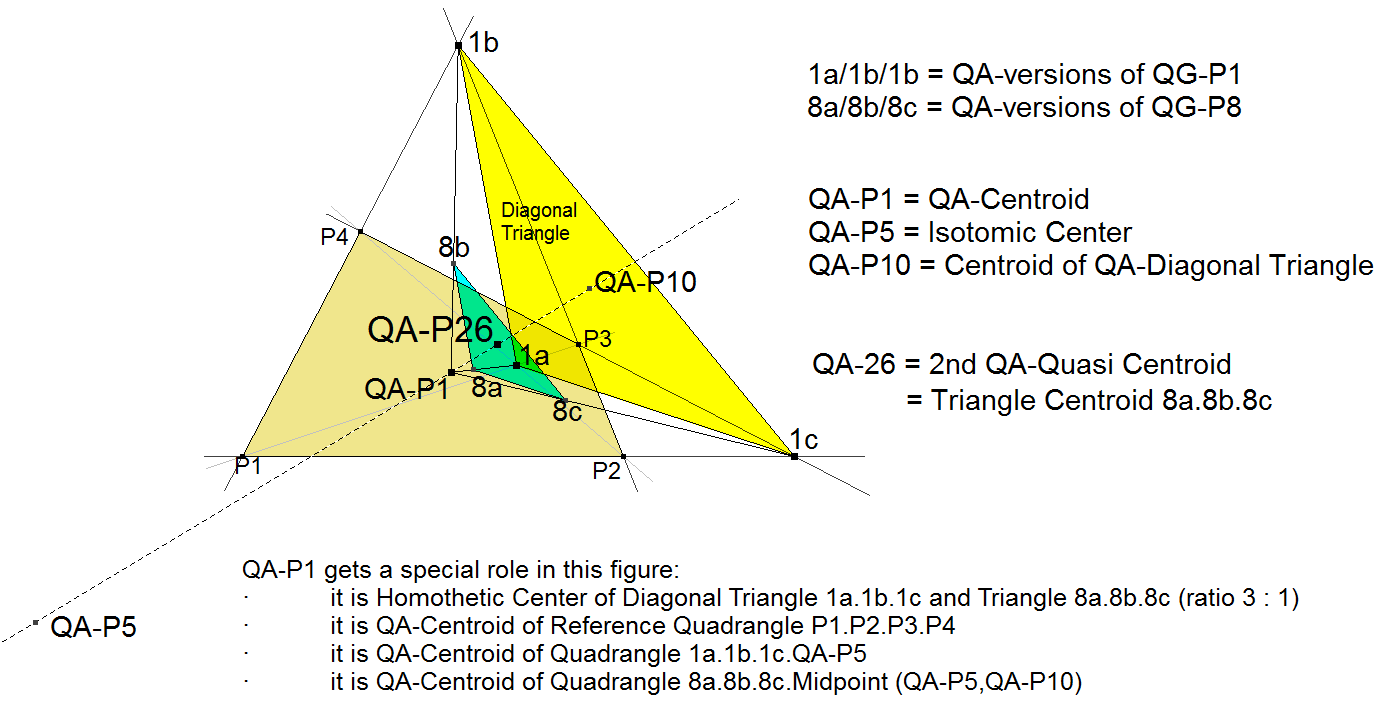
QA-P26: 2nd QA-Quasi Centroid

QA-P26 is the Centroid of the triangle formed by the 3 QA-versions of QG-P8 (2^nd Quasi Centroid), constructed in the QA-Quadrigons of a Reference Quadrangle.

1st CT-Coordinate

(q + r) (2 p + q + r) (5 p (p + q + r) + 3 q r)

1st DT-Coordinate

(q² – r²)² – p⁴ – 8 p² (-p² + q² + r²)

Properties

• QA-P26 lies on these lines:
  • QA-P1.QA-P5= QA-L3(-1 : 10)
  • QL-P12.QG-P8( 1 : 2)
• QA-P5.QA-P1 : QA-P1.QA-P26 : QA-P26.QA-P10 = 9 : 1 : 2.
• QA-P26 is the Reflection of QA-P25 in QA-P1.
• QA-P26 is the Centroid of the Triangle formed by the 3 QA-versions of QG-P8
• QA-P26 is the Centroid of the Triangle formed by the 3 QA-versions of QL-P12 (note Eckart Schmidt).
• QA-P26 is the Centroid of the Triangles formed by the 3 QA-versions of QG-P8.QL-P14.QL-P15 (all Centroid related points).
• QA-P26 is the Centroid of the Triangles formed by the 3 QA-versions of QA-P10.QG-P4.QG-P8 (all Centroid related points).
• QA-P26 is the Perspector of the QG-P8 Triple Triangle and the QL-P12 Triple Triangle (see QA-Tr-1).

Estimated human page views: 556