QL-1: Systematics for describing QL-Points
The method for describing points, lines, and other curves related to quadrilaterals involves referencing lines rather than points (as is done when describing a quadrangle). The major advantage of this approach is that all resulting algebraic expressions are symmetric.
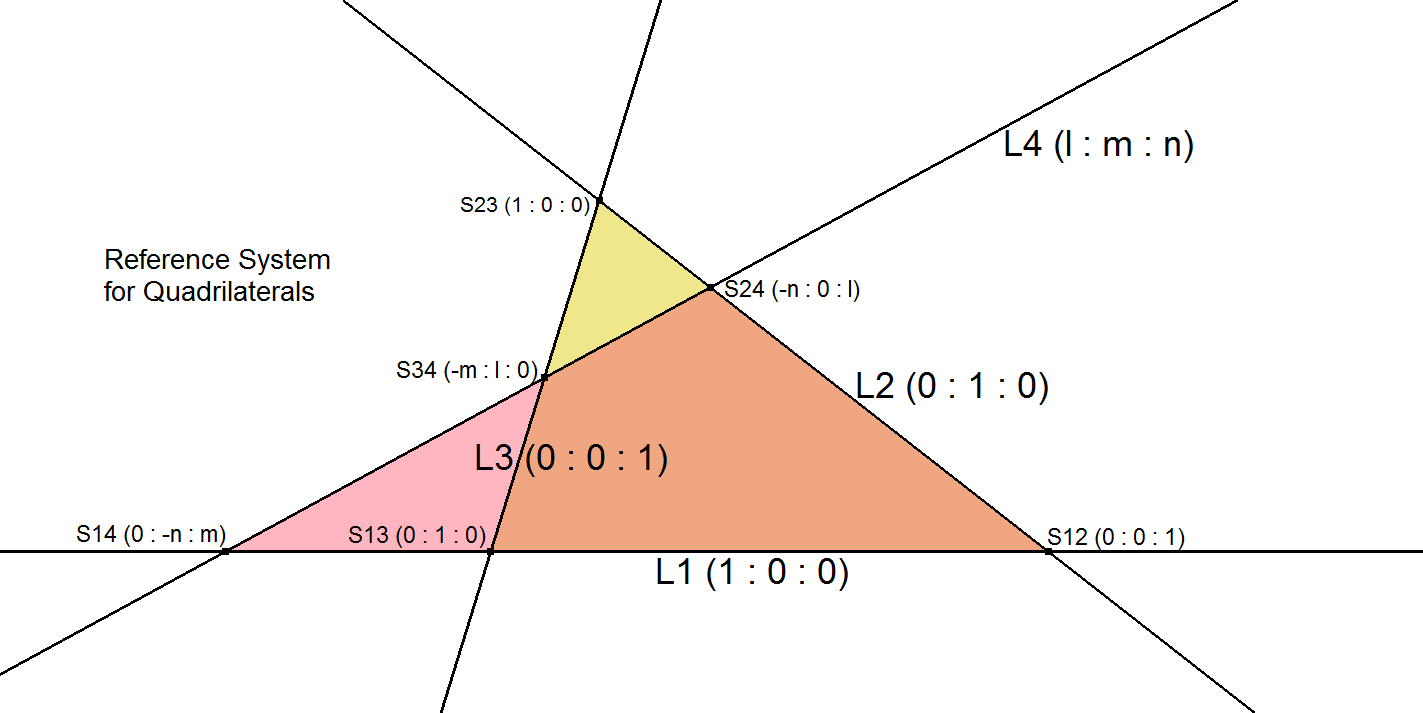
This system is based on three lines of the quadrilateral, represented with barycentric homogeneous coefficients:
- L₁:
(1:0:0) - L₂:
(0:1:0) - L₃:
(0:0:1)
The fourth line is assigned coefficients (l:m:n).
Note: The notation (l:m:n) is used for lines, whereas (p:q:r) is reserved exclusively for points.
Coordinate Systems Used
In this Encyclopedia of Quadri-Figures, two coordinate systems are used for quadrilaterals:
- QL-CT Coordinate System
Three arbitrary lines of the quadrilateral form a Component Triangle (CT). This triangle is defined as the reference triangle with line coefficients:(1:0:0)(0:1:0)(0:0:1)
The fourth line is then defined as
(l:m:n). - QL-DT Coordinate System
The QL-Diagonal Triangle (DT, see QL-Tr1) is defined as the reference triangle with the same line coefficients:(1:0:0)(0:1:0)(0:0:1)
An arbitrary line of the quadrilateral is defined as
(l:m:n). The remaining three lines now form the lines of the Anticevian Triangle with respect to the QL-Diagonal Triangle. Each lineLᵢacts as a perspectrix and has coefficients:(-l : m : n)(l : -m : n)(l : m : -n)
Both coordinate systems are interconvertible (see QL-6 and QL-7).
Every constructed object can now be identified as:
( f(a,b,c, l,m,n) : f(b,c,a, m,n,l) : f(c,a,b, n,l,m) )
where a,b,c represent the side lengths of the triangle with vertices P1 (1:0:0), P2 (0:1:0) and P3 (0:0:1).
In the description of the points on the following pages only the first of the 3 barycentric coefficients will be shown. The other 2 coordinates can be derived by cyclic rotations:
- a > b > c > a > etc.
- l > m > n > l > etc.
Further the Conway notation has been used in algebraic expressions:
- SA = (-a2 + b2 + c2) / 2
- SB = (+a2 – b2 + c2) / 2
- SC = (+a2 + b2 – c2) / 2
- Sω = (+a2 + b2 + c2) / 2
- S = √( SA SB + SB SC + SC SA) = 2 Δ
where Δ = area triangle ABC = ¼ √((a+b+c) (-a+b+c) (a-b+c) (a+b-c))
Triple Triangles / Triple Lines
The four lines L1, L2, L3, L4 in a Quadrangle can be placed in 3 different cyclic sequences.
These sequences are:
- L1 – L2 – L3 – L4,
- L1 – L2 – L4 – L3,
- L1 – L3 – L2 – L4.
Each of these 3 sequences represent a Quadrigon.
Just like a Quadrilateral has 4 Component Triangles, it also has 3 Component Quadrigons.
In these Component Quadrigons points can be constructed belonging to the domain of a Quadrigon or a Quadrangle. This gives us per Quadrilateral 3 versions of a Quadrigon Point / Quadrangle Point.
These 3 points form a Triple. The Triangle formed by this Triple is called the “QG-Px-Triple Triangle” or “QA-Px-Triple Triangle” in a Quadrilateral.
When the 3 points are collinear the Triple forms a Line called the “QG-Px-Triple Line” or “QA-Px-Triple Line” in a Quadrilateral.
Estimated human page views: 2014
