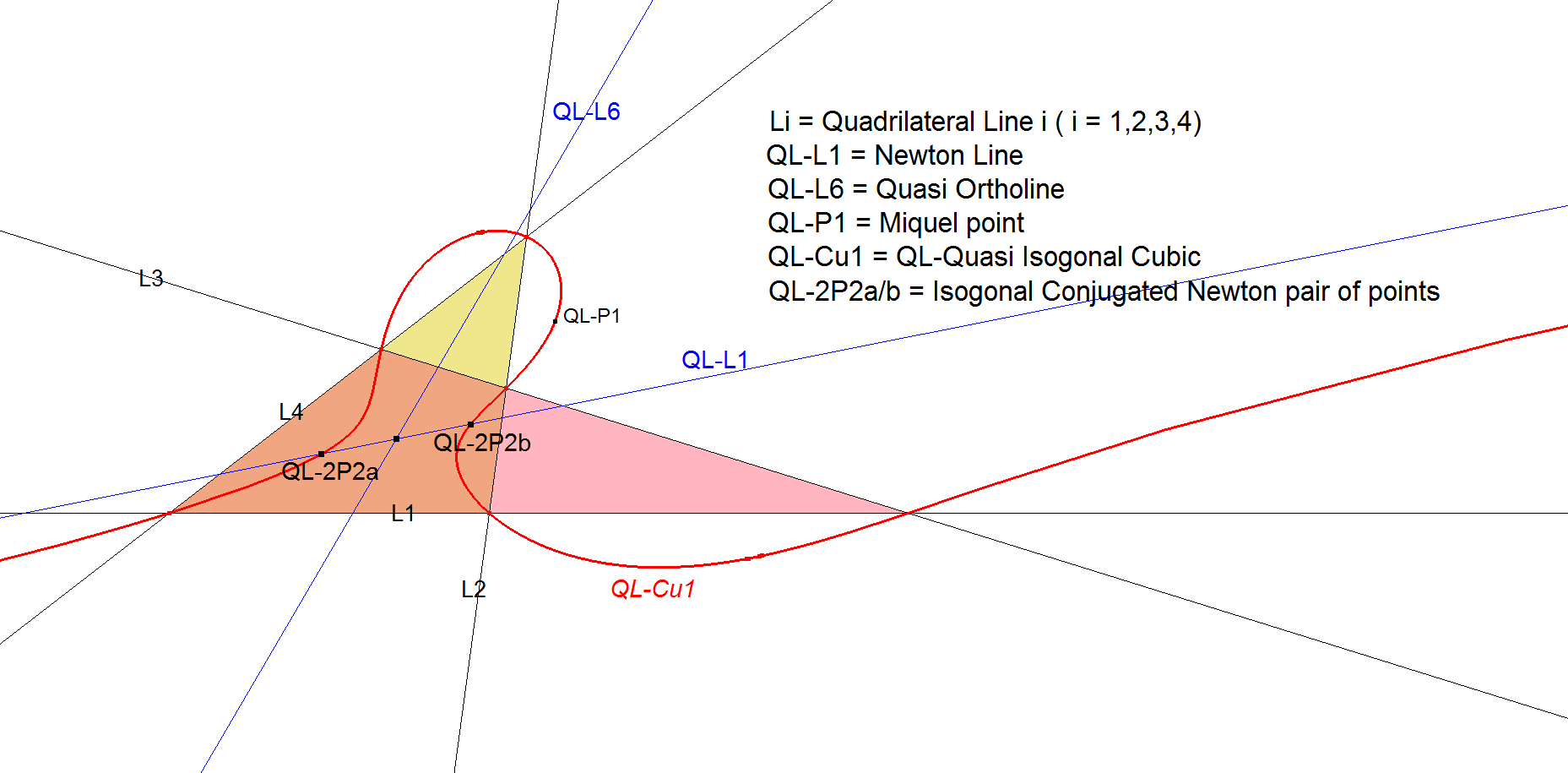
QL-2P2: Isogonal Conjugated Newton Pair of Points
There are exactly 2 points on the Newton Line that are each other’s IsogonalConjugate wrt all 4 QL-Component Triangles. These points lie on QL-Cu1. Their midpoint is the intersection point of the Newton Line QL-L1 and the Quasi Ortholine QL-L6. See [34], QFG # 179.
Under certain circumstances QL-2P2a & QL-2P2b can be imaginary points. Then also QL-Cu1 will be bi-partite (divided in two curves).
CT-Coordinates
(note: the + sign in front of the Square Root-part indicates different signs for QL-2P2a & QL-2P2b)
( (l (m – n) + m n) (a2 l2 m2 – b2 l2 m2 + c2 l2 m2 + 2 a2 l2 m n + 2 b2 l2 m n – 2 c2 l2 m n – 2 a2 l m2 n – 2 b2 l m2 n – 2 c2 l m2 n + a2 l2 n2 – b2 l2 n2 + c2 l2 n2 – 2 a2 l m n2 + 2 b2 l m n2 + 2 c2 l m n2 + a2 m2 n2 – b2 m2 n2 + c2 m2 n2
+ √(-4 b2 c2 (l2 (m – n)2 – m2 n2)2 + (b2 (l (m – n) + m n)2 + c2 (m n + l (-m + n))2 – a2 (m n – l (m + n))2)2)) :
-(-m n + l (m + n)) (a2 l2 m2 – b2 l2 m2 – c2 l2 m2 + 2 a2 l2 m n + 2 b2 l2 m n + 2 c2 l2 m n – 2 a2 l m2 n – 2 b2 l m2 n + 2 c2 l m2 n + a2 l2 n2 – b2 l2 n2 – c2 l2 n2 – 2 a2 l m n2 + 2 b2 l m n2 – 2 c2 l m n2 + a2 m2 n2 – b2 m2 n2 – c2 m2 n2
+ √ (-4 b2 c2 (l2 (m – n)2 – m2 n2)2 + (b2 (l (m – n) + m n)2 + c2 (m n + l (-m + n))2 – a2 (m n – l (m + n))2)2)) :
2 c2 (l (m – n) – m n) (l (m – n) + m n) (-m n + l (m + n)) )
Properties
- QL-2P2a & QL-2P2b lie on QL-L1, QL-Cu1.
- QL-2P2a & QL-2P2b are mutual QL-Tf1 images as well as QG-Tf2 images (Eckart Schmidt in [34], EQF message #217).
- The midpoint of QL-2P2a & QL-2P2b is the intersection point of QL-L1 ^ QL-L6.
- The circle through QL-2P2a & QL-2P2b and QL-P1 is the QL-Tf1 image of the Newton Line QL-L1 and is tangent at QL-Cu1 in QL-P1.
Estimated human page views: 789
