← Previous Next →

QL-Cu2: Eckart’s Cubic

QL-Cu2 is the Cubic that passes through the 27 centers of Morley’s Multi Cardioids. See QL-27Qu1. It was discovered by Eckart Schmidt (April, 2013). See [34] Quadri-Figures Group, message # 37 (first notification), #52, #56 (asymptotes // axes Deltoid), #57 (QL-P1), #58 (27 Cardioid Centers).

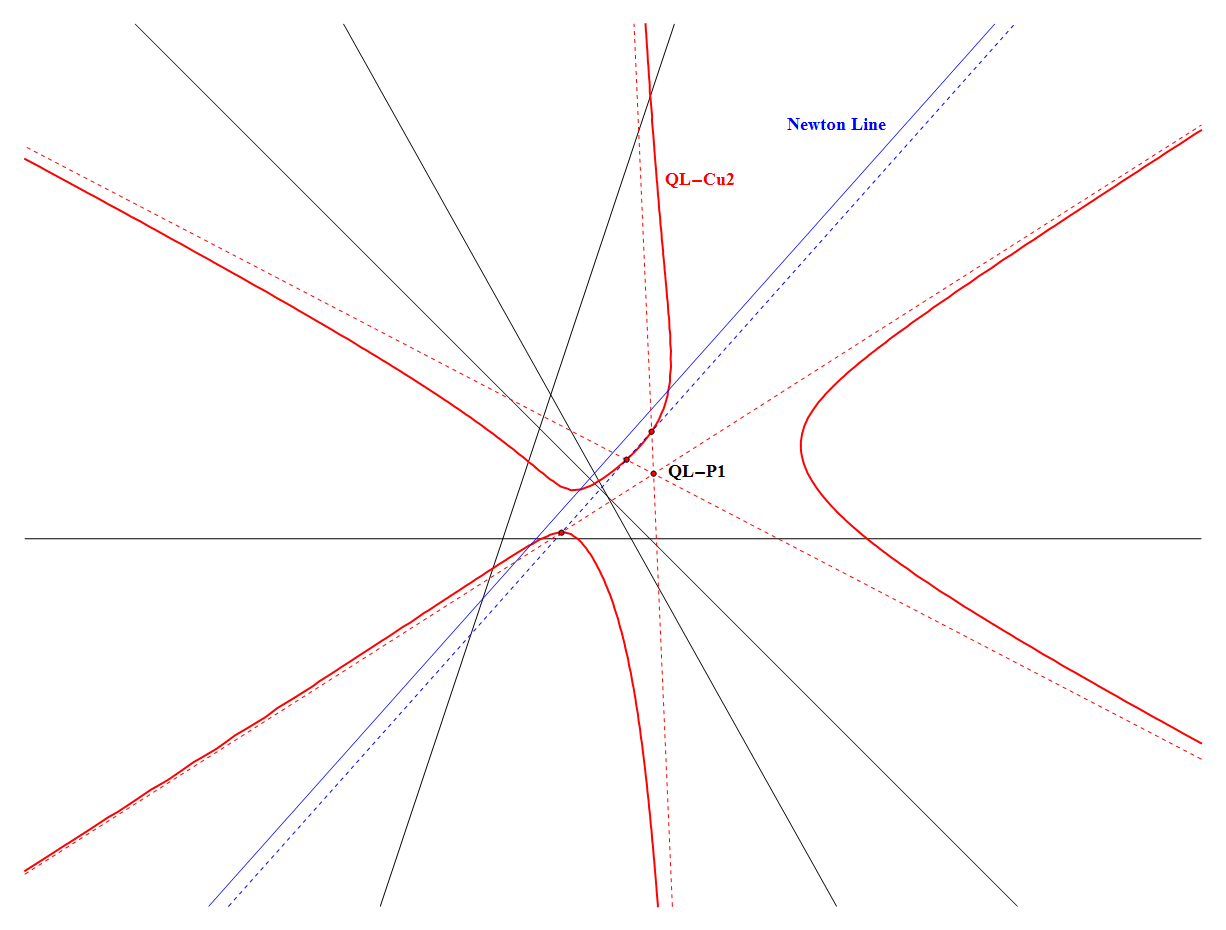
It’s three asymptotes meet in one point QL-P1 (Miquel Center) at angles of 60°.

The asymptotes are parallel to the three axes of the Kantor-Hervey Deltoid QL-Qu2.

The construction of QL-Cu2can be found at [34], QFG message # 558.

Bernard Gibert made a detailed description at [17d] in a paper he wrote on the basis of this special cubic.

More information about the cubic also can be found at [43].

Infovisual QL-Cu2-infovisual-cvt-01.gif
Equation in CT-notation

b2 c2 l (a2 ( l m + l n – m n) – b2 (m – l) (m – n) – c2 (n – l) (n – m)) x3

+ a2 c2 m (b2 ( l m – l n + m n) – c2 (n – l) (n – m) – a2 ( l – m) ( l – n)) y3

+ a2 b2 n (c2 (-l m + l n + m n) – a2 (l – m) ( l – n) – b2 (m – l) (m – n)) z3

+ 3 a2 b2 c2 (l x + m y) (m y+ n z) (n z + l x) = 0

Equation in DT-notation

(m4 Sa3 – 2 m2 n2 Sa3 + n4 Sa3 + 2 l2 m2 Sa2 Sb + 2 l2 n2 Sa2 Sb + 2 m2 n2 Sa2 Sb + 2 n4 Sa2 Sb + l4 Sa Sb2 + 6 l2 n2 Sa Sb2 + n4 Sa Sb2 + 2 l2 m2 Sa2 Sc + 2 m4 Sa2 Sc + 2 l2 n2 Sa2 Sc + 2 m2 n2 Sa2 Sc + 2 l4 Sa Sb Sc + 6 l2 m2 Sa Sb Sc + 6 l2 n2 Sa Sb Sc + 2 m2 n2 Sa Sb Sc + 4 l4 Sb2 Sc + 4 l2 n2 Sb2 Sc + l4 Sa Sc2 + 6 l2 m2 Sa Sc2 + m4 Sa Sc2 + 4 l4 Sb Sc2 + 4 l2 m2 Sb Sc2) (l2 x3 + 3 m2 x y2 + 3 n2 x z2)

+ (m4 Sa2 Sb + 6 m2 n2 Sa2 Sb + n4 Sa2 Sb + 2 l2 m2 Sa Sb2 + 2 l2 n2 Sa Sb2 + 2 m2 n2 Sa Sb2 + 2 n4 Sa Sb2 + l4 Sb3 – 2 l2 n2 Sb3 + n4 Sb3 + 4 m4 Sa2 Sc + 4 m2 n2 Sa2 Sc + 6 l2 m2 Sa Sb Sc + 2 m4 Sa Sb Sc + 2 l2 n2 Sa Sb Sc + 6 m2 n2 Sa Sb Sc + 2 l4 Sb2 Sc + 2 l2 m2 Sb2 Sc + 2 l2 n2 Sb2 Sc + 2 m2 n2 Sb2 Sc + 4 l2 m2 Sa Sc2 + 4 m4 Sa Sc2 + l4 Sb Sc2 + 6 l2 m2 Sb Sc2 + m4 Sb Sc2) ( m2 y3 + 3 l2 x2 y + 3 n2 y z2)

+ (4 m2 n2 Sa2 Sb + 4 n4 Sa2 Sb + 4 l2 n2 Sa Sb2 + 4 n4 Sa Sb2 + m4 Sa2 Sc + 6 m2 n2 Sa2 Sc + n4 Sa2 Sc + 2 l2 m2 Sa Sb Sc + 6 l2 n2 Sa Sb Sc + 6 m2 n2 Sa Sb Sc + 2 n4 Sa Sb Sc + l4 Sb2 Sc + 6 l2 n2 Sb2 Sc + n4 Sb2 Sc + 2 l2 m2 Sa Sc2 + 2 m4 Sa Sc2 + 2 l2 n2 Sa Sc2 + 2 m2 n2 Sa Sc2 + 2 l4 Sb Sc2 + 2 l2 m2 Sb Sc2 + 2 l2 n2 Sb Sc2 + 2 m2 n2 Sb Sc2 + l4 Sc3 – 2 l2 m2 Sc3 + m4 Sc3) (n2 z3 + 3 l2 x2 z + 3 m2 y2 z)

+ 3 (m6 Sa3 – m4 n2 Sa3 – m2 n4 Sa3 + n6 Sa3 + 3 l2 m4 Sa2 Sb + 2 l2 m2 n2 Sa2 Sb + 3 m4 n2 Sa2 Sb + 3 l2 n4 Sa2 Sb + 2 m2 n4 Sa2 Sb + 3 n6 Sa2 Sb + 3 l4 m2 Sa Sb2 + 3 l4 n2 Sa Sb2 + 2 l2 m2 n2 Sa Sb2 + 2 l2 n4 Sa Sb2 + 3 m2 n4 Sa Sb2 + 3 n6 Sa Sb2 + l6 Sb3 – l4 n2 Sb3 – l2 n4 Sb3 + n6 Sb3 + 3 l2 m4 Sa2 Sc + 3 m6 Sa2 Sc + 2 l2 m2 n2 Sa2 Sc + 2 m4 n2 Sa2 Sc + 3 l2 n4 Sa2 Sc + 3 m2 n4 Sa2 Sc + 6 l4 m2 Sa Sb Sc + 6 l2 m4 Sa Sb Sc + 6 l4 n2 Sa Sb Sc – 4 l2 m2 n2 Sa Sb Sc + 6 m4 n2 Sa Sb Sc + 6 l2 n4 Sa Sb Sc + 6 m2 n4 Sa Sb Sc + 3 l6 Sb2 Sc + 3 l4 m2 Sb2 Sc + 2 l4 n2 Sb2 Sc + 2 l2 m2 n2 Sb2 Sc + 3 l2 n4 Sb2 Sc + 3 m2 n4 Sb2 Sc + 3 l4 m2 Sa Sc2 + 2 l2 m4 Sa Sc2 + 3 m6 Sa Sc2 + 3 l4 n2 Sa Sc2 + 2 l2 m2 n2 Sa Sc2 + 3 m4 n2 Sa Sc2 + 3 l6 Sb Sc2 + 2 l4 m2 Sb Sc2 + 3 l2 m4 Sb Sc2 + 3 l4 n2 Sb Sc2 + 2 l2 m2 n2 Sb Sc2 + 3 m4 n2 Sb Sc2 + l6 Sc3 – l4 m2 Sc3 – l2 m4 Sc3 + m6 Sc3) x y z

Properties
  • These points lie on QL-Cu2:
    • the 27 centers of Morley’s Multiple Cardioids QL-27Qu1.
  • It’s three asymptotes meet in QL-P1 (Miquel Center) at angles of 60°.
  • The asymptotes are parallel to the three axes of the Kantor-Hervey Deltoid QL-Qu2 (Eckart Schmidt, May 9, 2013).
  • The intersection points of QL-Cu2 with its three asymptotes lie collinear on a line parallel to QL-L1 (Newton Line) in 2/3 distance to QL-P1 (Miquel Point).
  • See [34], QFG message # 94 (Eckart Schmidt, June 29, 2013).


Estimated human page views: 842

Scroll naar boven