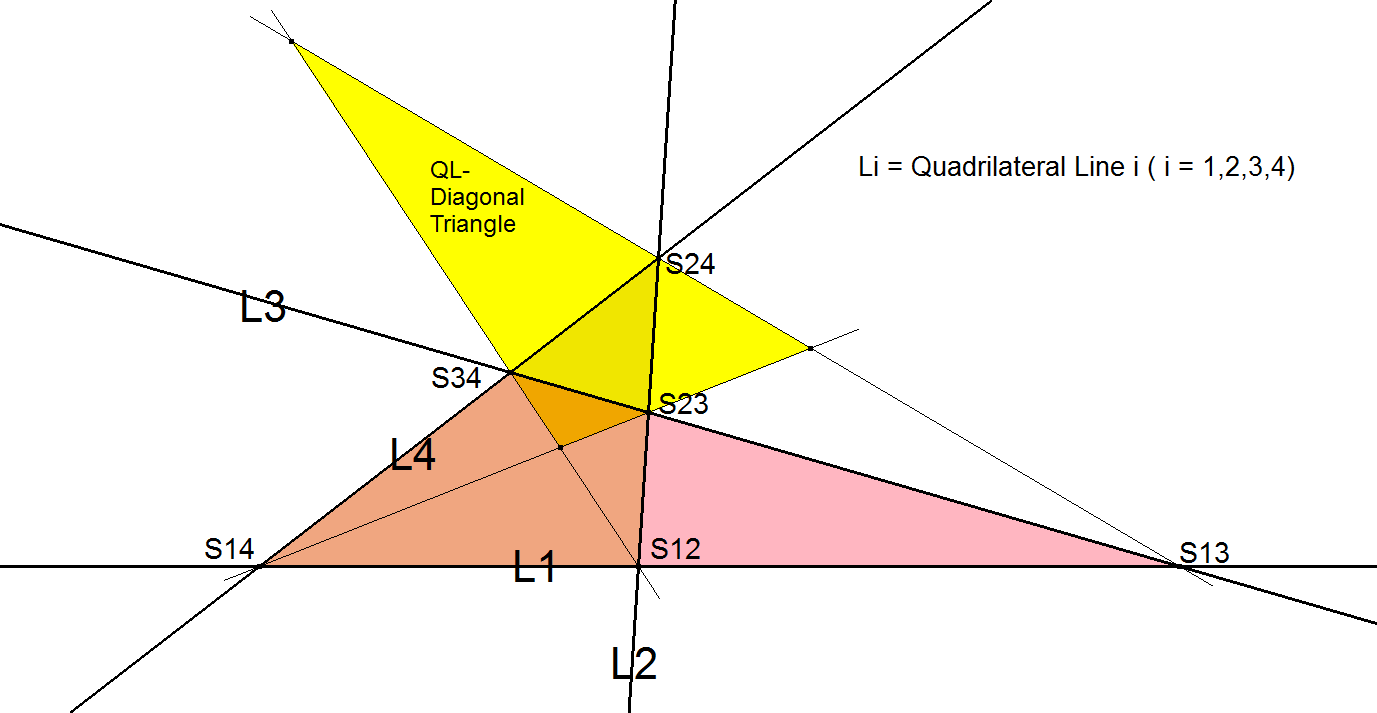
QL-Tr1: QL-Diagonal Triangle

The Diagonal Triangle of the Quadrilateral (L1, L2, L3, L4) is the Triangle bounded by lines S12.S34, S13.S24, S14.S23, where Sij = intersection point Li ^ Lj, where i and j are different numbers and ∈ (1,2,3,4).

The connection of the intersection points of 2 adjacent lines and the intersection point of the remaining 2 lines produces a side of the QL-Diagonal Triangle. By doing this for all 3 possible combinations of 2 sets of 2 adjacent lines the QL-Diagonal Triangle is produced.

Area QL-Diagonal Triangle in CT-notation

4 l² m² n² Δ / ((l m – l n – m n) (l m + l n – m n) (l m – l n + m n))

Radius² Circumcircle QL-Diagonal Triangle in CT-notation

l² m² n² (a² l² – a² l m – b² l m + c² l m + b² m²) (a² l² – a² l n + b² l n – c² l n + c² n²) (b² m² + a² m n – b² m n – c² m n + c² n²)  /  (4 Δ² (l m – l n – m n)² (l m + l n – m n)² (l m – l n + m n)²)

Area QL-Diagonal Triangle in DT-notation

S / 2

Radius² Circumcircle QL-Diagonal Triangle in CT-notation

a² b² c² / (4 S²)

Properties

• The QL-Diagonal Triangle is the AntiCevian Triangle of each of the 4 Component Triangles Li.Lj.Lk, where Ll is the perspectrix and where (i,j,k,l) ∈ (1,2,3,4).
• QL-Tr1 is self-polar wrt every conic inscribed in the Reference Quadrilateral.

Estimated human page views: 563