← Previous Next →

CU-6P-cDe1 CU-inscribed Complete Decagon

In a similar way as the construction of the CU-inscribed Complete Hexagon it is possible to inscribe a Complete Decagon into a cubic using just six starting points.

Definitions

Definition 1: A decagon, or 10-gon, is a geometrical figure composed of 10 consecutive vertices, no three of them being collinear.

Definition 2: A complete decagon is a geometric figure formed by 10 consecutive vertices, no three of them being collinear and additionally including the intersection points of the 5 pairs of opposite sides.

In other words, a complete hexagon consists of 10 consecutive vertices and the points of intersection of the 5 pairs of opposite sides, creating a set of 15 points of the Reference Cubic.

Theorem: A complete decagon can be inscribed in a cubic curve using only six initial points.

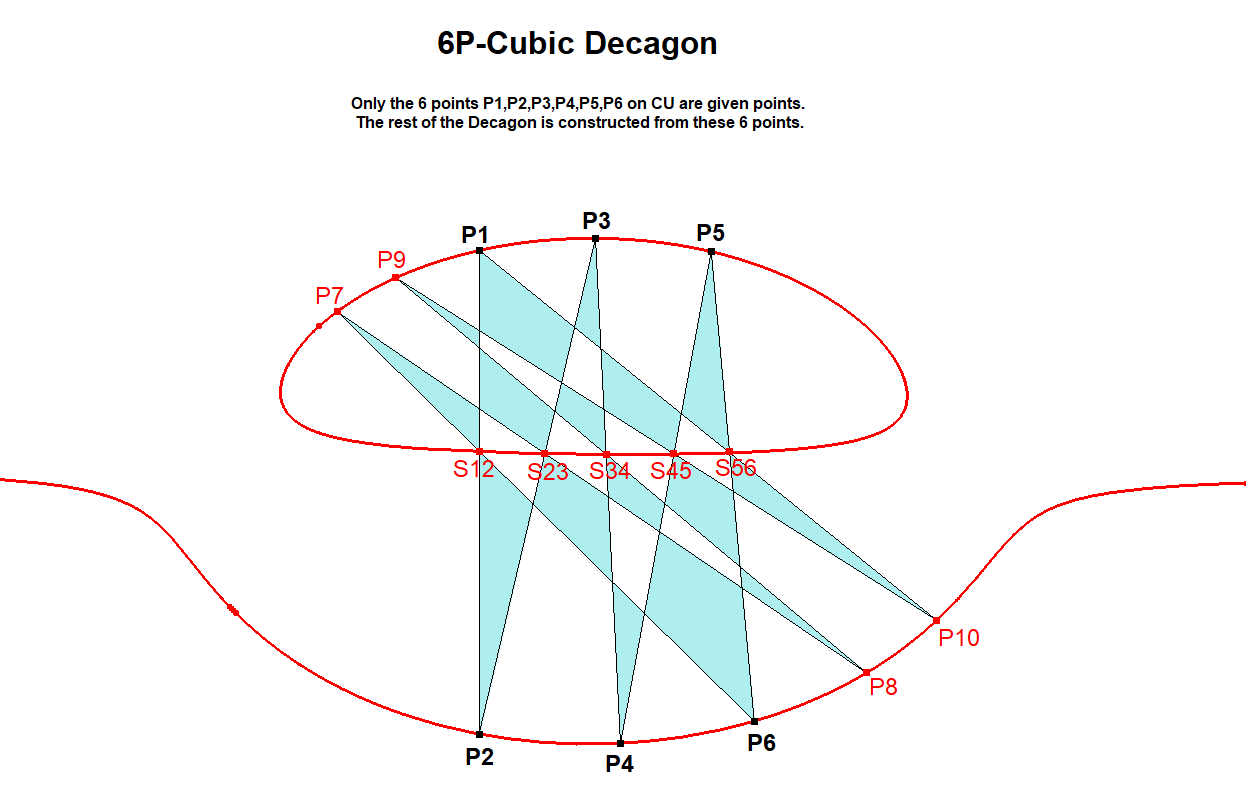
Infovisual CU-6P-cDe1-infovisual-cvt-01.png

CU-6P Cubic Decagon-02.fig

Construction

The procedure to construct the CU-inscribed Decagon (10-gon) using 6 random points on CU is:

  1. Start with 6 random points P1,P2,P3,P4,P5,P6 on a reference cubic CU.
  2. Draw line P1P2 intersecting CU again in S12.
  3. Draw line P2P3 intersecting CU again in S23,
  4. Draw line P3P4 intersecting CU again in S34,
  5. Draw line P4P5 intersecting CU again in S45,
  6. Draw line P5P6 intersecting CU again in S56,
  7. Draw line P6S12 intersecting CU again in P7,
  8. Draw line P7S23 intersecting CU again in P8.
  9. Draw line P8S34 intersecting CU again in P9,
  10. Draw line P9S45 intersecting CU again in P10.
  11. Draw line P10S56 intersecting CU again in P1 !

Last step easily can be proven using the CU Point Addition Method CU-4:

CU Point Validation
  1. Use the property that for 3 collinear points P, Q, and R, the sum P + Q + R = N.
  2. S12 = N – P1 – P2
  3. S23 = N – P2 – P3
  4. S34 = N – P3 – P4
  5. S45 = N – P4 – P5
  6. S56 = N – P5 – P6
  7. P7 = N – P6 – S12 = N – P6 – (N – P1 – P2) = P1 + P2 – P6
  8. P8 = N – P7 – S23 = N – P7 – (N – P2 – P3) = P2 + P3 – P7
  9. P9 = N – P8 – S34 = N – P8 – (N – P3 – P4) = P3 + P4 – P8
  10. P10 = N – P9 – S45 = N – P9 – (N – P4 – P5) = P4 + P5 – P9
  11. Px = N – P10 – S56 = N – P10 – (N – P5 – P6) = P5 + P6 – P10 = P5 + P6 – (P4 + P5 – P9) = P6 + P9 – P4 = P6 + (P3 + P4 – P8) – P4 = P3 + P6 – P8 = P3 + P6 – (P2 + P3 – P7) = P6 + P7 – P2 = P6 + (P1 + P2 – P6) – P2 = P1
Construction of 2-Gon/6-Gon/10-Gon/etc.

Extrapolating, it appears that there is a CU-inscribed 2P-2-gon, 4P-6-gon (Hexagon), 6P-10-gon (Decagon), 8P-14-gon, etc.

Construction of a CU-inscribed 4P-6-gon in a more general way:

  1. Start with 4 random points P(1),P(2),P(3),P(4) on the reference cubic CU.
  2. Draw lines P(i)P(i+1) intersecting CU in S(i,i+1) for i=1,2,3
  3. Draw lines P(i+3)S(i,i+1) intersecting CU in P(i+4) for i=1,2,3

Finally P(7) coincides with P(1).

Similar construction of a CU-inscribed (n+1)P-2n-gon, valid for n=3,5,7, etc.

  1. Start with n+1 random points P(1),…,P(n+1) on a cubic CU.
  2. Draw lines P(i)P(i+1) intersecting CU in S(i,i+1) for i=1,..,n
  3. Draw lines P(i+n)S(i,i+1) intersecting CU in P(i+n+1) for i=1,…,n

Finally P(2n+1) coincides with P(1).

This also can be proven using the CU Point Addition Method CU-4.

4-Gons/8-Gons/12-Gons/etc.

Note that using the same procedure for a CU-inscribed 3P-4-gon, 5P-8-gon, 7P-12-gon, etc. it doesn’t deliver the original starting point:

In the case of a 3P-4-gon, P5 doesn’t coincide with P1, like it does with the 4P-hexagon and 6P-decagon, etc.

However P1P5 is the Tangential of P3.

In the case of a 5P-8-gon, P9 doesn’t coincide with P1, like it does with the 4P-hexagon and 6P-decagon, etc.

However P1P9 is the Tangential of P5. This also can be proven using the CU Point Addition Method CU-4.



Estimated human page views: 6

Scroll naar boven