CU-9P-3P1 IP-SumPoints of the set (P1,…,P9)
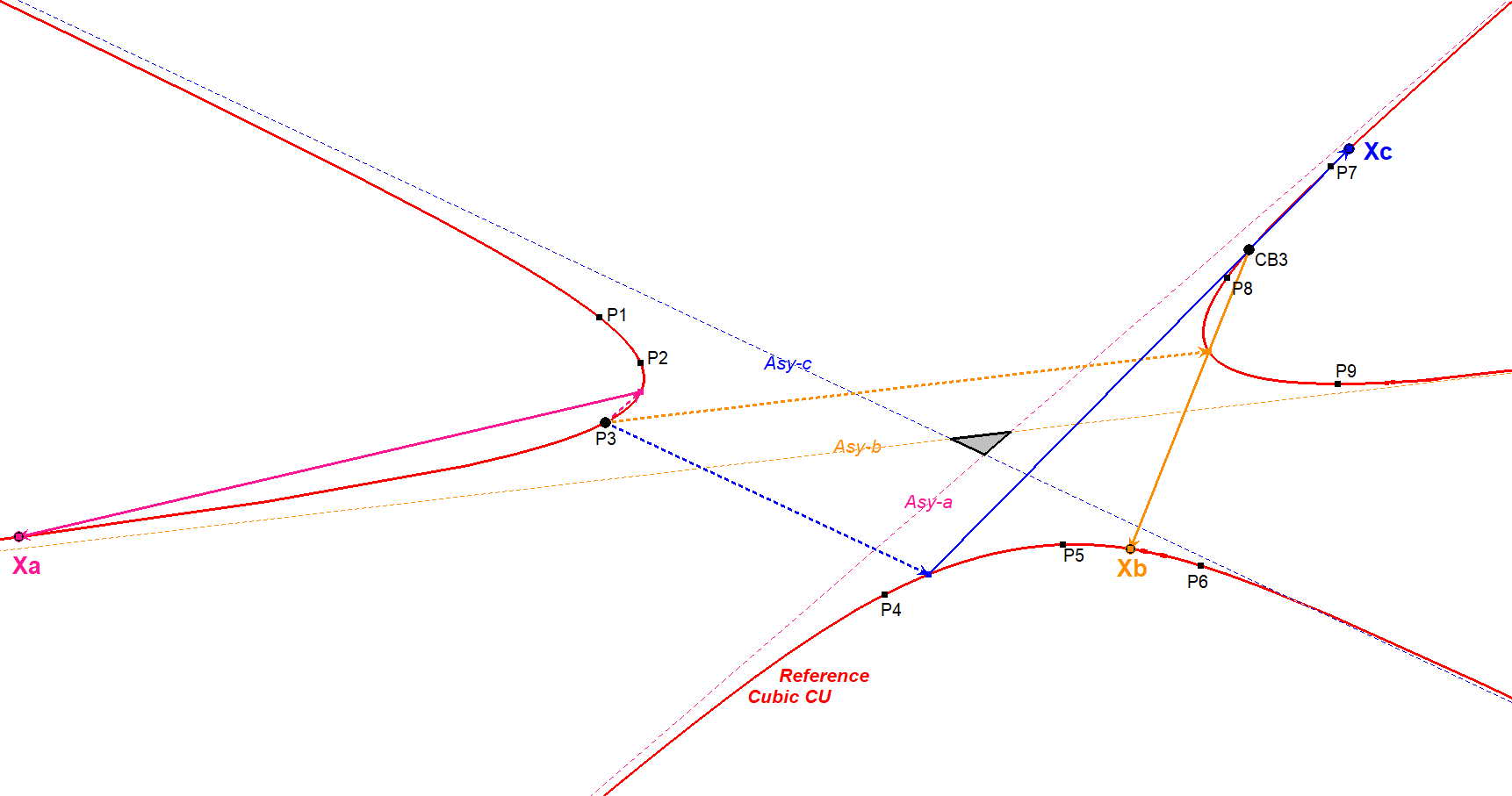
Given reference cubic CU with 9 random points P1, …, P9 on CU.
Let aPi be the 2nd intersection point of CU with the Asy-a-Parallel through Pi (i=1,…,9).
Xa = aPi.CBi, which is a fixed point for i=1, … , 9.

CU-9P-3P1 IP-Sumpoints of the set (P1,…,P9)-01.fig
Validation:
Calculation for IPa and CB9:
P1 + P2 + P3 + P4 + P5 + P6 + P7 + P8 + CB9 = 3N(1)
P9n + P9 + IPa = N(2)
CB9 + P9n + Xa = N(3)
From (1) and (2) and (3) it follows that:
Xa = IPa + PP9 -3N, where PP9 = P1 + P2 + P3 + P4 + P5 + P6 + P7 + P8 + P9
In the same way there are fixed points Xb and Xc, when there are 3 real CU-asymptotes.
Xa, Xb, Xc are the IPa/b/c-Sumpoints of the set (P1,…,P9).
CU-9P-3P1 IP-Sumpoints of the set (P1,…,P9)-10.fig
Estimated human page views: 118
