CU-9P1 Set of 9 Flexpoints of the Cubic

Each Cubic has 9 Flexpoints, also known as Flexes.

They are the inflection points of the cubic. An inflection point is a point on the curve where the curvature changes – either from increasing to decreasing or vice versa.

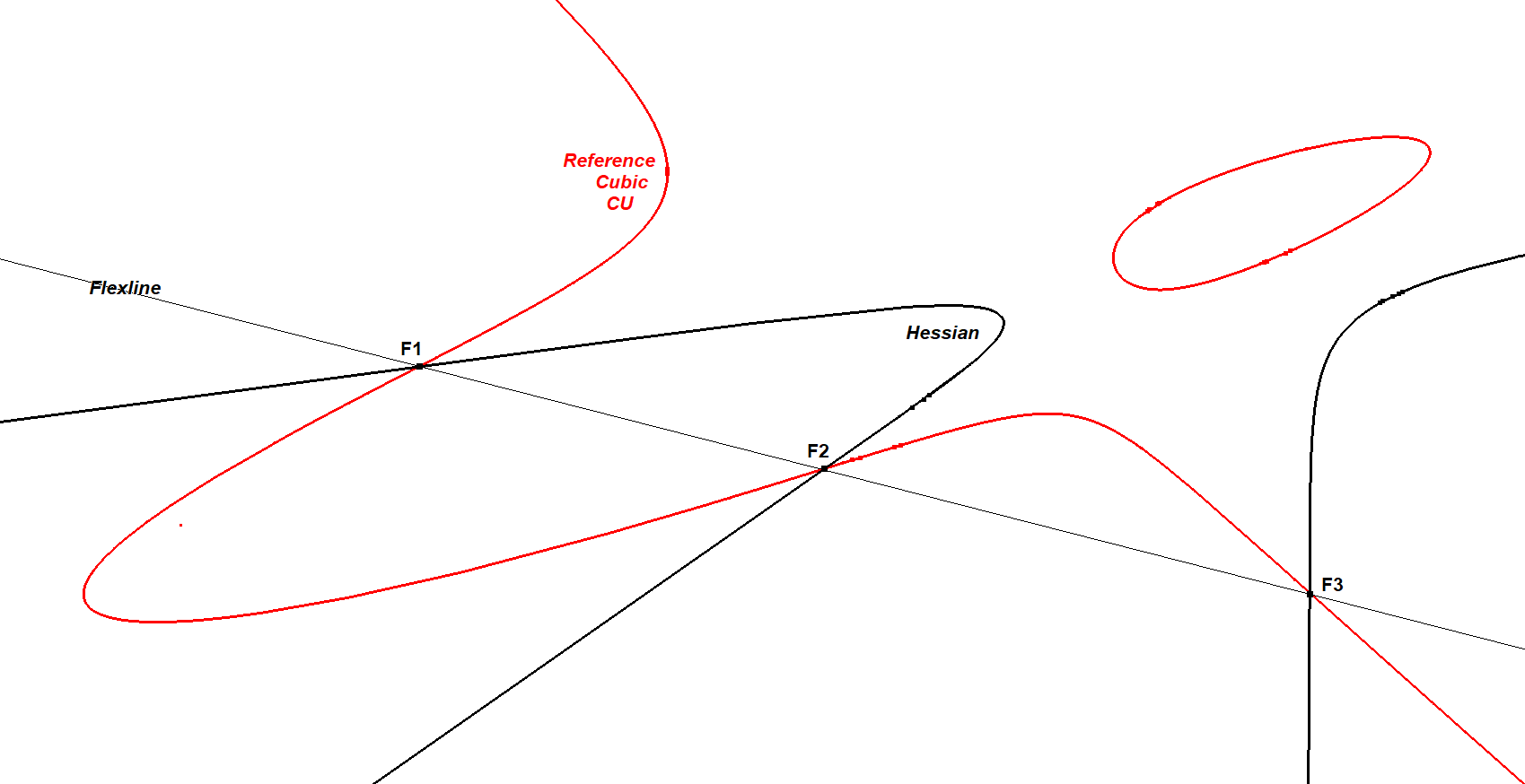
Flex points are the intersection points of the cubic CU with its Hessian curve, which is also of degree three (see CU-Cu1). Therefore there are nine such intersections, corresponding to the nine inflection points.

Of these nine inflection points, three are real and six are imaginary. The three real points are always collinear (see also CU-12L1).

CU-12L1a Real Flexline-01

Quick construction to approximate the 3 real flexpoints (QPG#2046)

This is based on Schröter’s book [82], page 242.

Start with an arbitrary point F on the cubic with three secants,

… which give 3×2 cubic intersections,

… if they are coconic on a conic CO, then F is an inflection point.

Construction of the 3 real flexpoints

The standard method for determining the 3 real flex points is by drawing the Hessian of CU. Refer to CU-Cu1 for details.

The Hessian is also a cubic. Consequently, the Reference Cubic CU and its Hessian intersect at nine points. These points constitute the nine flex points, of which only three will be real and collinear.

Network of the 9 flexpoints

There is an entangled network of 9 flexpoints and 12 connecting flexlines with 3 points per line and 4 lines per points. See CU-12L1.

Estimated human page views: 7