CU-IP-3Tf1 Set of 3 Quasi-Möbius Transformations (QMT)

There exist at every Cubic 3 Quasi-Miquel Triangles with each 3 vertices (CU-IP-3P1). Some of them are real, others are imaginary points depending on the shape of the cubic.

Nevertheless each vertex is the center of a Quasi-Möbius Transformation (QMT). Of course the real vertices are appealing because they are visible in the real plane and so are the real QMT’s.

Each QMT maps a point on the cubic to another point on the cubic. It is often described that these points are ‘swapped.’ Additionally, it is stated that the cubic is invariant with respect to the QMT, meaning that the QMT maps any point on the cubic to another point on the cubic.

There are two main ways of construction for these QMT’s.

1. The limited and straightforward construction, which only works for points on the cubic.
2. The extended and intricate construction, which not only works for points on the cubic but also involves points outside of the cubic. It swaps points on the cubic in the same way as the limited construction does.

The limited construction

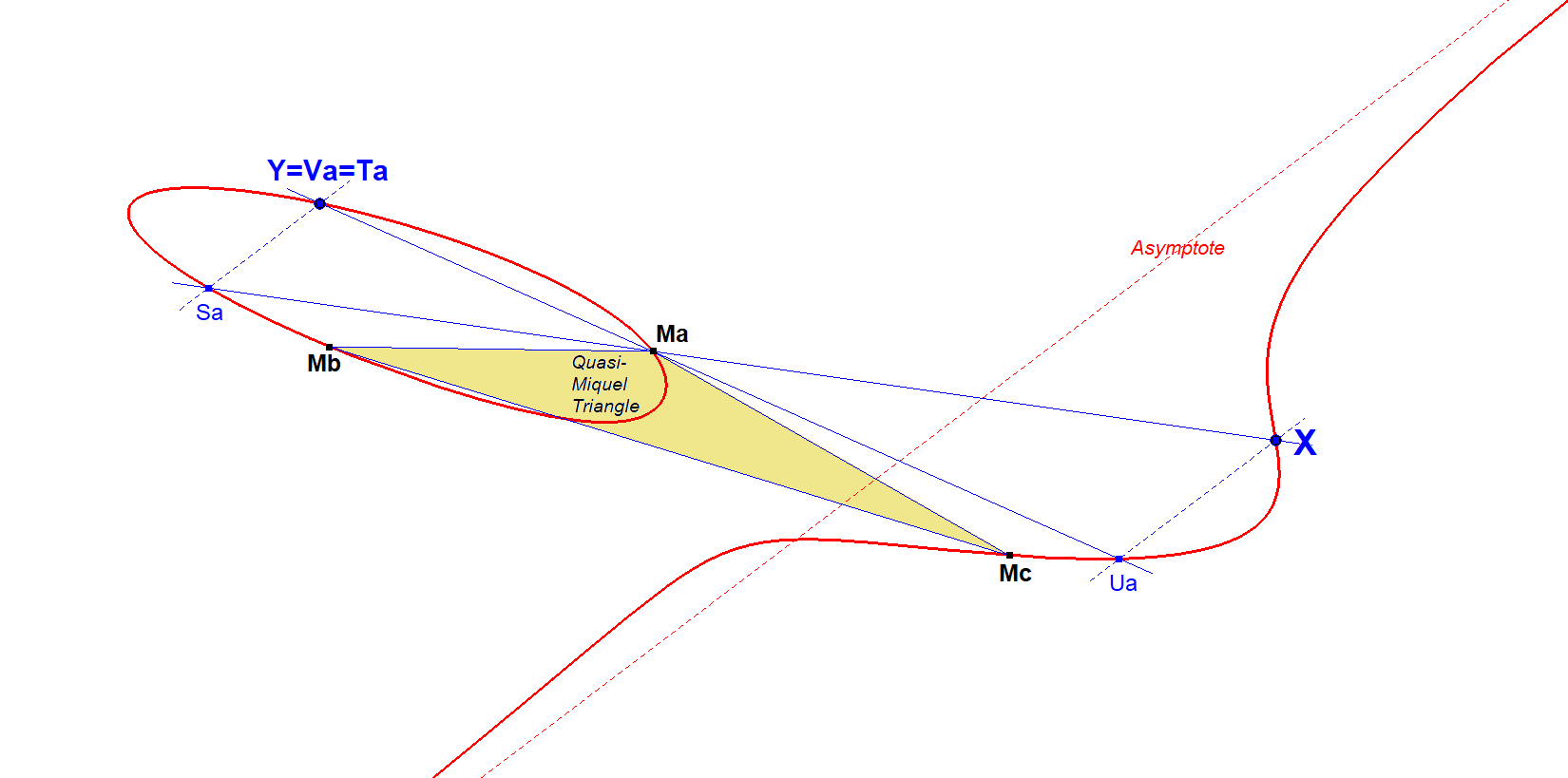
We will choose one of the vertices of the three Quasi-Miquel Triangles to illustrate our construction.

Each Quasi-Miquel Triangle is associated with one of the asymptotes. Let’s designate our vertex as being related to asymptote-1, abbreviated as Asy1, and identify it as the ‘a-vertex.’ Therefore, we will refer to our vertex as Ma. The construction will be carried out with this vertex as the center. Let X be the point to be swapped into Y.

Now the construction is very simple:

1. Draw XMa and let Sa be the 3^rd intersection point of XMa with the cubic.
2. Draw a line through Sa parallel to Asy1 and let Ta be the 2^nd finite intersection point of this parallel line with the cubic (the 3^rd intersection point will be the infinity point of the asymptote).
3. Then Y=Ta is the point of transformation.

There is even a resembling alternative for this construction:

1. Draw a line through X parallel to Asy1 and let Ua be the 2^nd finite intersection point of this parallel line with the cubic (the 3^rd intersection point will be the infinity point of the asymptote).
2. Draw MaUa and let Va be the 3^rd intersection point of MaUa with the cubic.
3. Then Y=Va=Ta is the point of transformation.

This ‘trapezium-construction’ only holds when a Quasi-Miquel Point is center of the trapezium.

CU-IP-Tf1-Quasi-Moebius Transformation-01.fig

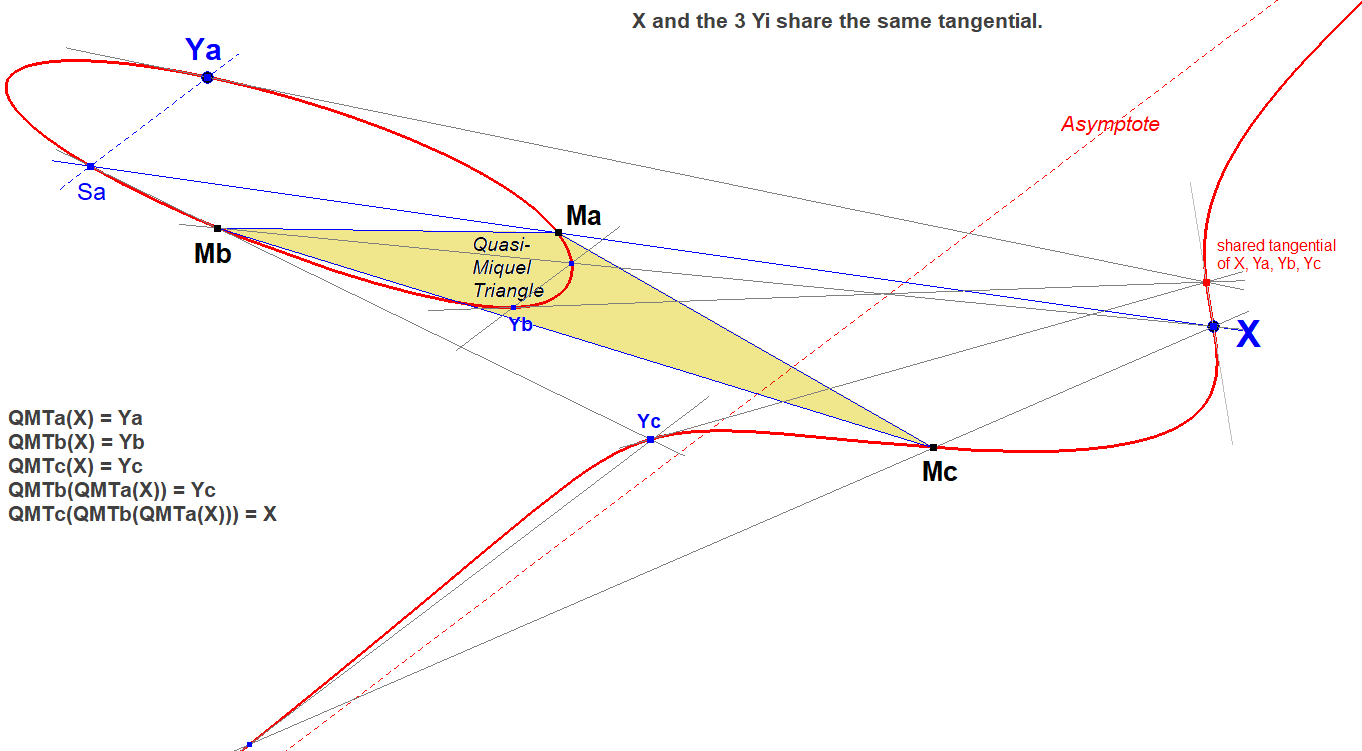
Note that vertex has its own point of transformation mapped by QMTa, QMTb, QMTb.

Let’s call the mapped points Ya, Yb, Yc.

1. X, Ya, Yb, Yc share the same tangential.
2. QMTc(QMTb(QMTa(X))) = X

CU-IP-Tf1-Quasi-Moebius Transformation-02.fig

The extended construction

There exist(s) at every Circular Cubic 1 or 3 Quasi-Miquel Point(s). See CU-IP-3P1, special case ‘Circular Cubics’.

Each of their vertices is the center of a Möbius Transformation.

This Möbius Transformation maps a point by inversion about a circle with center M (Quasi-Miquel Point) completed with a reflection about an axis through M.

There is an equivalent for this Möbius Transformation for the general cubic called the Quasi-Möbius-Transformation (abbreviated by ‘QMT’).

The difference is that a Quasi-Möbius-Transformation maps a point by inversion about a conic with center M completed with a reflection about an axis through M.

It is found and developed at QPG.

The inverse wrt a conic

For this we must define the notion of the inverse X of a point P wrt a conic.

For a circle we draw a half-line from O (the center of the circle) to P intersecting the circle in S, and measuring X on half-line OP such OS² = OP * OX.

For a conic we do exactly the same: we draw a half-line from O (the center of the conic) to P intersecting the conic in S, and measuring X on half-line OP such OS² = OP * OX.

Construction of the Quasi-Möbius-Transformation CU-IP-3Tf1(P)

Given a bipartite reference cubic CU.

This cubic has 3 asymptotes, from which at least one is real.

Choose a real asymptote.

Anallagmatic Points

There are 4 points P1, P2, P3, P4 on the cubic where the tangent is parallel to this asymptote.

These points are called the Anallagmatic points (see CU-IP-4P1). Some of these points can be imaginary.

They are anallagmatic because these points are the center of a circle inverting each point on CU in another point on CU. This actually is only the case when the cubic is circular (having the circular points at infinity on it).

However here we extent the definition of Anallagmatic to being also the center of a conic inverting each point on CU in another point.

Inversion conic and anti-inversion conic

3 of the 4 anallagmatic points are centers of an “inversion conic”, meaning that the 2 other CU-intersection points of each line through this center lie inverse wrt the conic.

1 of the 4 anallagmatic points is center of an “anti-inversion conic”, meaning that the 2 other intersection points of each line through this center lies inverse wrt the conic and will then be reflected about the center.

Therefore this single point has a special status.

Let’s denote the anallagmatic point with the special status P1 and the other 3 anallagmatic points P2, P3, P4.

Note: On a circular cubic this point is the incenter of the Diagonal Triangle of QA(P1,P2,P3,P4) and the other 3 anallagmatic points are the excenters of the Diagonal Triangle of QA(P1,P2,P3,P4).

Inversion conics

Each anallagmatic point is center of an “(anti-)inversion conic”.

Denote these conics with center P1,P2,P3,P4 as Co1, Co2, Co3, Co4.

These conics are similar (same eccentricity) and have parallel axes.

Their positioning is quasi-orthogonal, meaning that per set of two crossing conics (let’s say Co1 and Co2) the 2 Co1-tangents at their intersection points intersect in the center of Co2 and vice versa.

Co1, Co2, Co3, Co4 have a quasi-orthogonal positioning, which appears to be a condition to mutually combine pairwise these conics.

Pairwise intersecting of the inversion conics

Like mentioned they pairwise intersect in two real intersection points, defining a Radical Axis.

Denote the intersection points of Co1 and Co2 as F12a&F12b, etc.

The 4 conics can mutually cross 6 times.

All 6 radical axes pass through P1.

Furthermore the 3 mutual radical axes of Co2, Co3, Co4 pass through some extra points.

Summarizing:

• F12a-F12b only passes through P1
• F13a-F13b only passes through P1
• F14a-F14b only passes through P1
• F23a-F23b passes through P1, P4, M14
• F24a-F24b passes through P1, P3, M13
• F34a-F34b passes through P1, P2, M12

Where M12, M13, M14 are the vertices of the Diagonal Triangle of QA(P1,P2,P3,P4).

Pairwise combining the inversion conics

Inversion conics can be pairwise combined into another conic, which is called the mutual product of these two inversion conics.

Let Co1 and Co2 be two inversion-conics and INV1 and INV2 the inversion-transformations wrt Co1 and Co2. Let Co12 be the product-inversion-conic Co1xCo2 and INV12 the inversion-transformations wrt Co12.

Now CO12 is the conic for which INV12(X) = INV1(INV2(X)) = INV2(INV1(X)).

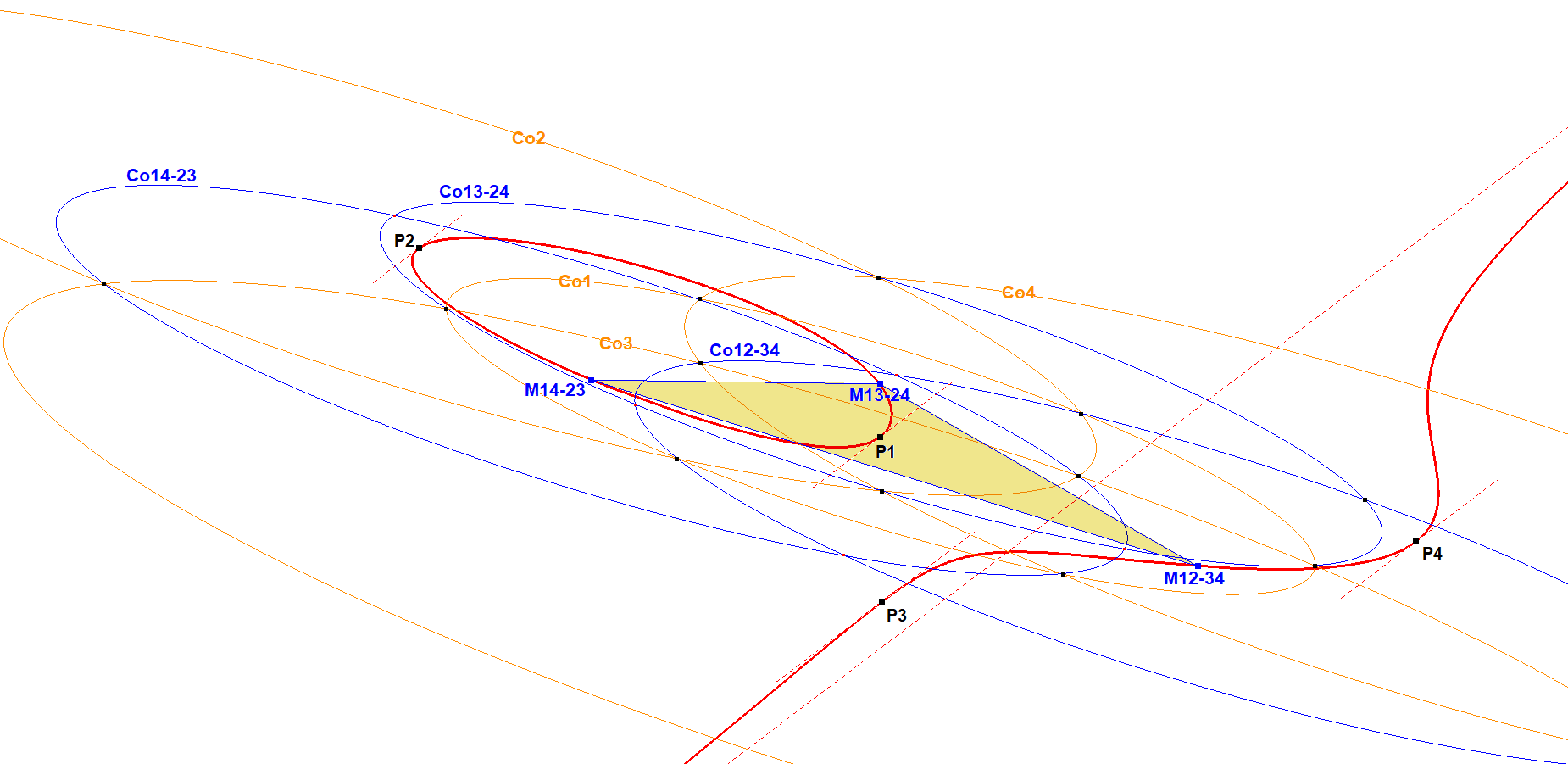
It appears that wrt inversion-conics Co1, Co2, Co3, Co4 that Co12=Co34, Co13=Co24, Co14=Co23. Therefore we will call these inversion-conics resp. Co12-34, Co13-24, Co14-23 with resp. centers M12-34, M13-24, M14-23:

Specifications of these product conics are:

Co12-34 = Co1 x Co2 as well as Co3 x Co4

• with center M12-34=P1P2xP3P4,
• passing through the intersection points of Co3xCo4 (with tangents parallel to P3P4)
• passing through the intersection points of Co1xCo2 (with tangents through P2)
• with QMT-axis=P1P2 and QMT-target-point=infinity point P3P4.

Co13-24 = Co1 x Co3 as well as Co2 x Co4

with center M13-24=P1P3xP2P4,

• passing through the intersection points of Co2xCo4 (with tangents parallel to P2P4)
• passing through the intersection points of Co1xCo3 (with tangents through P3)
• with QMT-axis=P1P3 and QMT-target-point=infinity point P2P4.

Co14-23 = Co1 x Co4 as well as Co2 x Co3

• with center M14-23=P1P4xP2P3,
• passing through the intersection points of Co2xCo3 (with tangents parallel to P2P3)
• passing through the intersection points of Co1xCo4 (with tangents through P4)
• with QMT-axis=P1P4 and QMT-target-point=infinity point P2P3.

CU-IP-3P1a-Quasi-Miquel Triangle-25-Trf-Conics

Construction of the product conics

Since we know the center of these 3 product conics, as well as their axes and in all cases 4 intersection points on it, the product conics can easily be constructed.

Definition Quasi-Möbius Transformation

Since we know the center of these 3 product conics, as well as their axes we also can define the Quasi-Möbius Transformations as being the (anti-)inverse in a given product conic completed by the reflection about the given axis.

Quasi-Möbius Transformations (QMT’s) wrt product-conics

Denote the Quasi-Möbius-Transformation wrt product-conic Co12-34 by QMT12-34.

QMT12-34(P) = INV2(AINV1(P)) = AINV1(INV2(P)) = INV3(INV4(P)) = AINV4(INV3(P)), where

• AINV1(P) is the Anti-Inverse of P wrt Conic1 (with center P1),
• INV2(P) is the Inverse of P wrt Conic2 (with center P2),
• INV3(P) is the Inverse of P wrt Conic3 (with center P3),
• INV4(P) is the Inverse of P wrt Conic4 (with center P4).

Similar rules are valid for QMT13-24(P) wrt Co13-24 and QMT14-23(P) wrt Co14-23.

Properties of the QMT’s

So finally we have three QMT’s:

• QMT12-34 swaps (P1,P2), (P3,P4), (M13-24,M14-23)
  • wrt conic Co12-34 with center M12-34,
  • with QMT-axis P1P2 and QMT-target-point=infinity point P3P4.
• QMT13-24 swaps (P1,P3), (P2,P4), (M12-34,M14-23)
  • wrt conic Co13-24 with center M13-24,
  • with QMT-axis P1P3 and QMT-target-point=infinity point P3P4.
• QMT14-23 swaps (P1,P4), (P2,P3), (M12-34,M13-24)
  • wrt conic Co14-23 with center M14-23,
  • with QMT-axis P1P4 and QMT-target-point=infinity point P2P3.

Apart from the mentioned swapping-pairs also all points on the cubic can be swapped with other points on the cubic, as well as points not on the conic can be swapped with other points not on the cubic.

See these QPG-messages #1968, #1971-#1974, #1983-#2020, #2026, #2028-#2031 by Bernard Keizer, Eckart Schmidt and Chris van Tienhoven where you can find the discussion that caused above theory.

Properties

• QMT’s on a general cubic map lines and conics into conics
• QMT’s on a circular cubic map lines into circles and map circles into lines.
• QPG#1795: X and X’ have the same tangential.
• QPG#1791: for a bipartite circular cubic there are three of this transformations giving for a cubic point P three images P1, P2, P3. The points P, P1, P2, P3 have the same tangential.

QMT’s on Circular Cubics

In QPG#1862 there is a resumé about a QMT on the circular cubic with two branches.

It is full of special properties.

Here are the results.

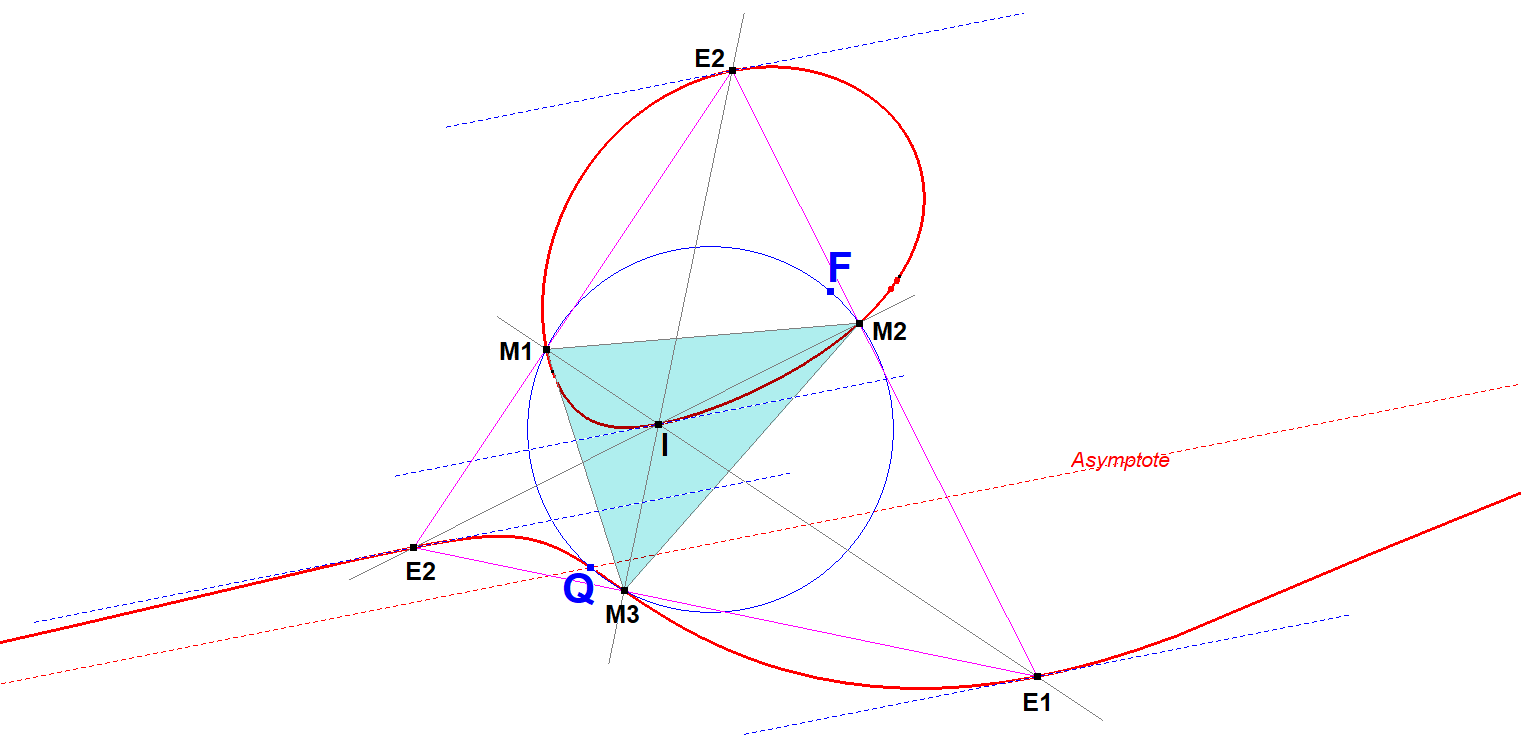
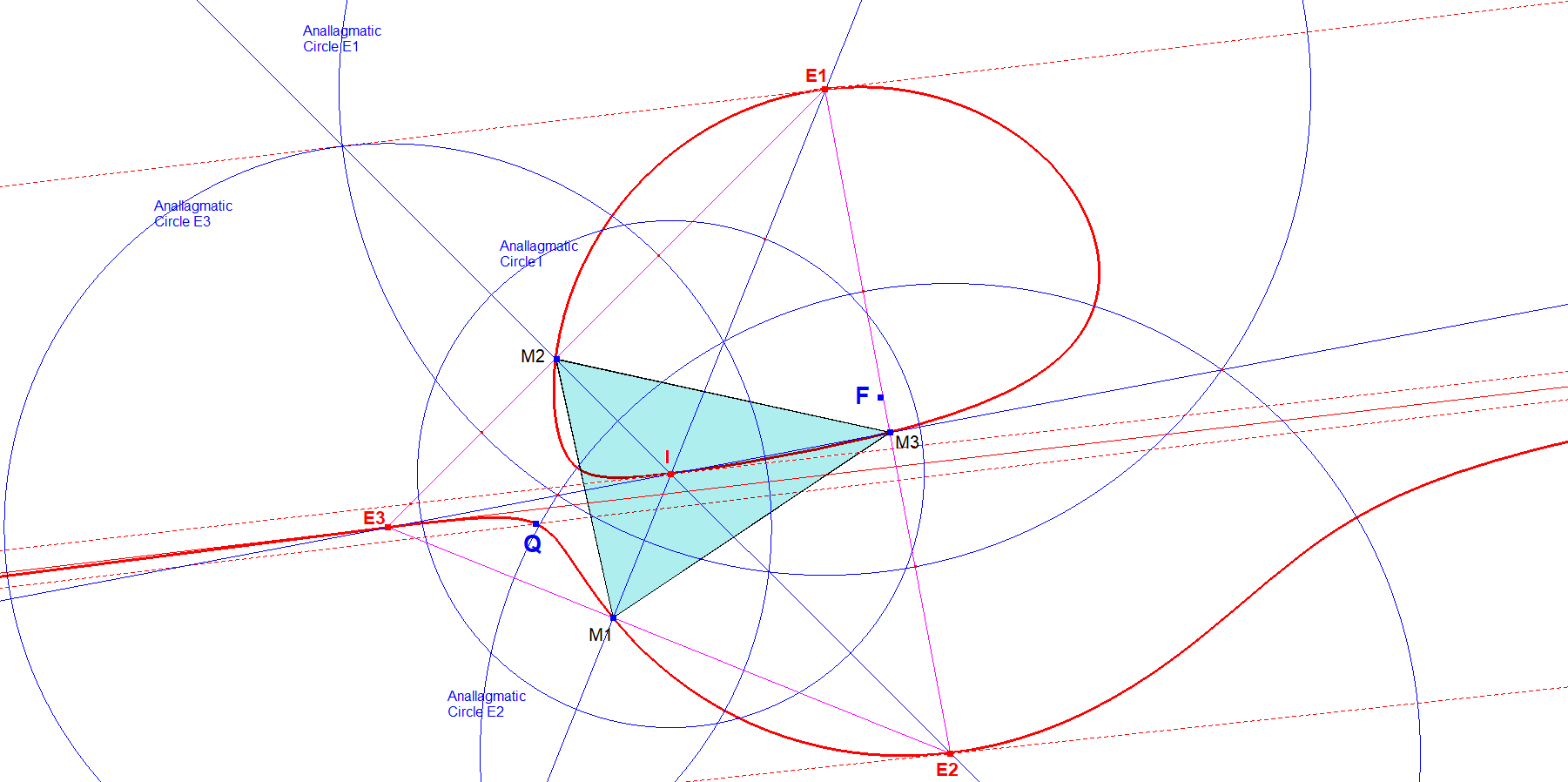
• Given a Bipartite Circular Cubic CUc2.
• CUc2 has a Focus F and an asymptote intersecting CUc2 in Q.
• CUc2 has a unique Miquel Triangle M1M2M3 lying on CUc2 and the circle with diameter FQ.

CUc2-4P In- and Excenters Miquel Triangle-03.fig

• Every vertex M1, M2 and M3 is the center of a Moebius Transformation Tf1, Tf2, Tf3, described by Bernard in QPG#1795.
• Let m1, m2, m3 be the lengths of the sides of triangle M1M2M3. Let r1, r2, r3 be the radius of Moebius-config-circles around M1, M2, M3.
• Tf1 swaps (M2,M3). Tf2 swaps (M3,M1). Tf3 swaps (M1,M2).
• Therefore r1*r1 = m2*m3,    r2*r2 = m3*m1,    r3*r3 = m1*m2.
• Also   m1*r1*r1 = m2*r2*r2 = m3*r3*r3 = m1*m2*m3.
• Because of 6. the axes of the transformations are the internal angle bisectors of the Miquel Triangle. Consequently the perpendiculars of the axes in M1, M2, M3 are the external angle bisectors.
• The internal and external bisectors of the Miquel Triangle intersect in the incenter I and excenters E1, E2, E3 of the Miquel Triangle. These are all points of CUc2.
• The tangents at I, E1, E2, E3 are lines parallel to the CUc2-asymptote.
• All points on CUc2 lie within two strokes bounded by 2 times 2 of these tangents. The oval part in one stroke, the unlimited part in the other stroke.
• I, E1, E2, E3 lie all on the IP-Polar Conic of CUc2 (IP=Infinity Point of CUc2), which is the Orthogonal Hyperbola, described by Eckart in QPG#837/#1538. This allows for an easy construction of this Orthogonal Hyperbola.

Estimated human page views: 3