CU-IP-Co1 IP-Diametral Conic / IP-Polar Conic
CU-IP-Co1 is the Polar Conic of one of an infinity point of a reference cubic CU.
It contains the infinity point of the reference cubic it refers to, which makes it a hyperbola with one asymptote in common with CU.
There are 3 versions of the IP-Diametral Conic, for each infinity point there will be one version.
Two of these versions can be imaginary.
When CU has just 1 real asymptote, then there will be just 1 real IP-Diametral Conic.
When CU has 3 real asymptotes, then there will be 3 real IP-Diametral Conics.
It is mentioned by Roger Cuppens in a general context for general cubics and called by him “Conique Diamétrale”. See [63], page 262.
Construction
- Draw 5 lines parallel to one chosen asymptote each having a set of 2 finite intersection points with CU.
- The conic through the 5 midpoints of the sets of the 2 finite intersection points will be the IP-Diametral Conic corresponding to the chosen asymptote.
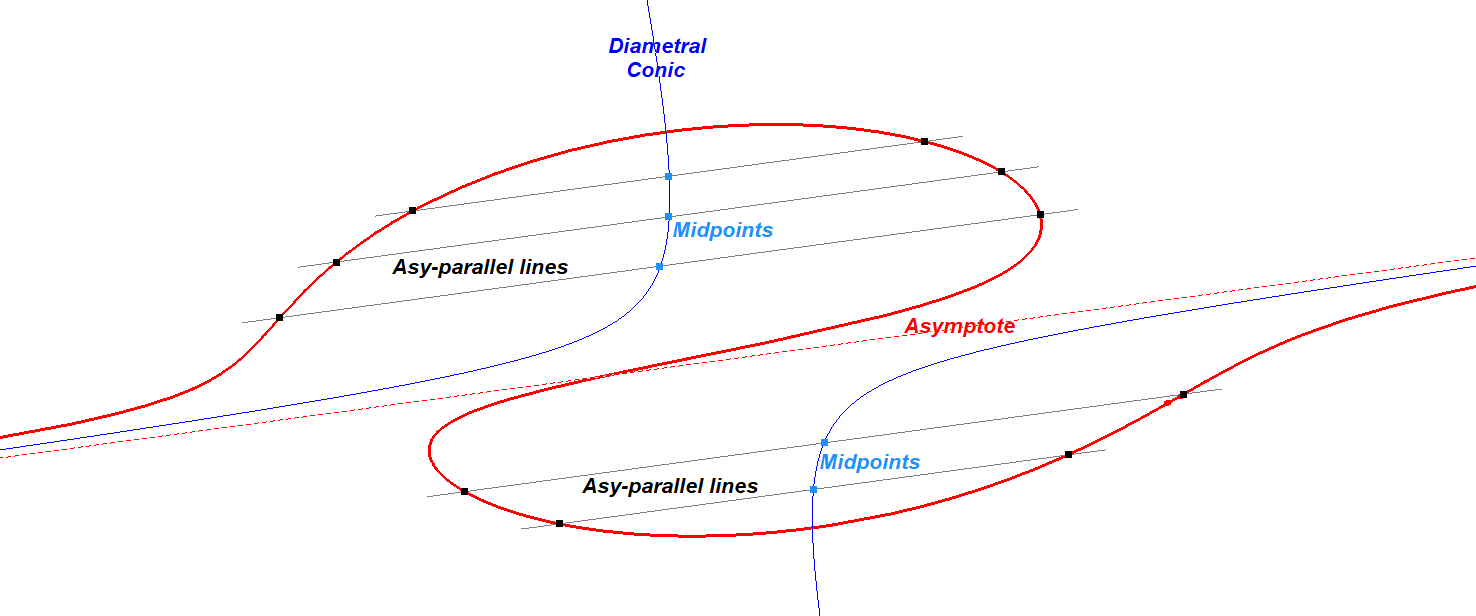
CU-IP-Co1 DiametralConic-Construction-01.fig
Properties
- CU-IP-Co1 is the locus of midpoints of the 2 intersection points of Asy-parallel lines with CU.
- The Asy-parallel line that coincides with the asymptote will deliver as intersection points twice the CU-Infinity point. Their midpoint will be the CU-Infinity point. Therefore each version of CU-IP-Co1 will share the CU-asymptote it refers to.
- The 3 versions of CU-IP-Co1 share 4 common points. These points have the special property that they are midpoint of 2 finite intersection points of any line parallel to a CU-asymptote. See QPG#1897.
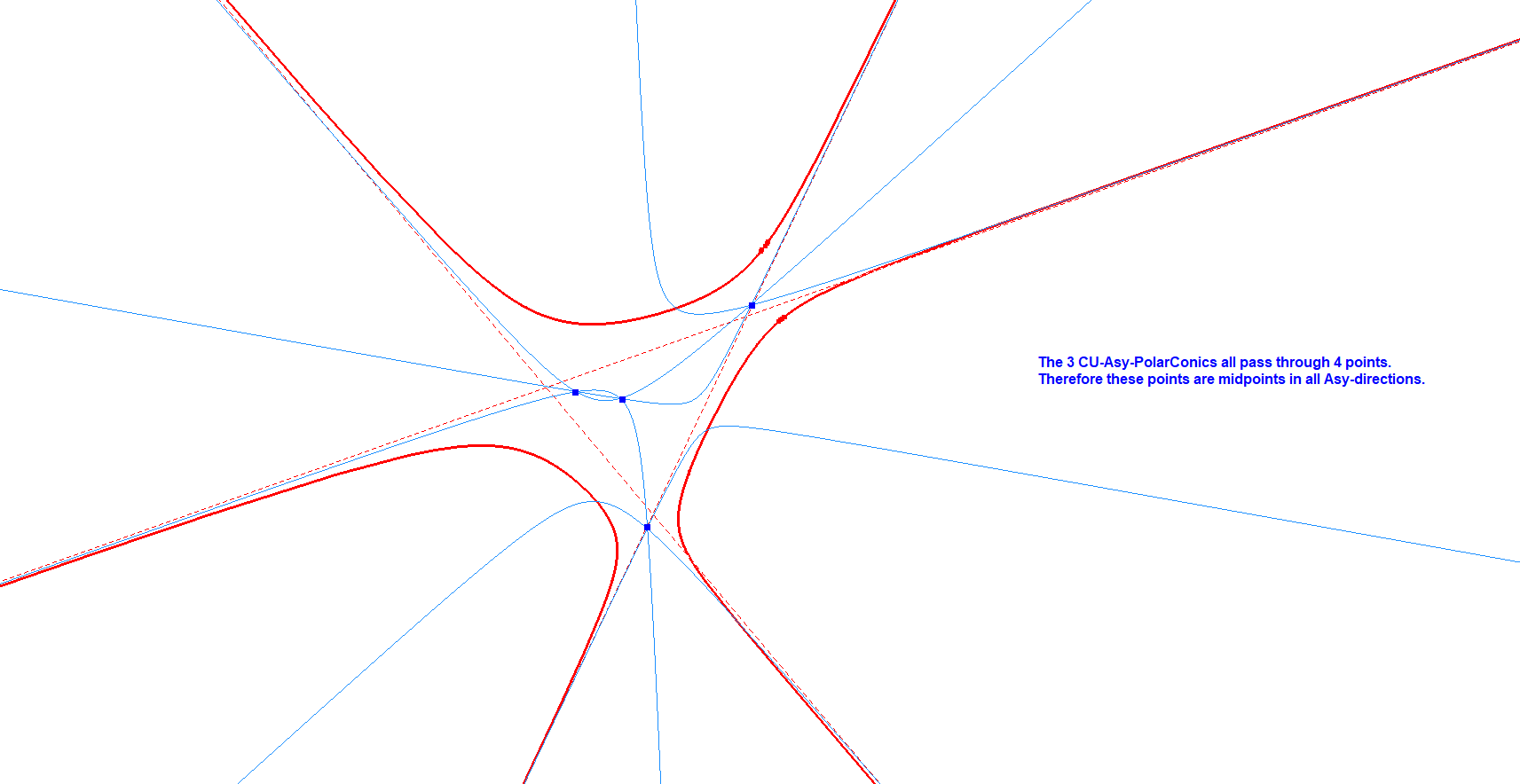
CU-IP-Co1 Set of 3 CU-DiametralConics-13.png
- Each version of CU-IP-Co1 cuts CU in the 4 anallagmatic points CU-IP-4P1 where the parallels of an asymptote touch the cubic. Two of these points can be imaginary.
Case Circular Cubic
On a circular cubic CU-IP-Co1 is an orthogonal hyperbola.
In the context of a circular cubic 7P-s-Cu1 it was mentioned by Eckart Schmidt in QPG-message #837.
Given a bipartite circular cubic CUc with 5 points as 5P, the remaining two points (Pi,Pj) give a fixed cubic pivot P = Pi.5P-s-Tf6(Pi) ^ Pj.5P-s-Tf6(Pj).
The line P.5P-s-P4 is parallel to the asymptote of 7P-s-Cu1.
Therefore parallels to P.5P-s-P4 intersect the cubic in two finite points, whose midpoints give the orthogonal hyperbola 7P-s-Co1.
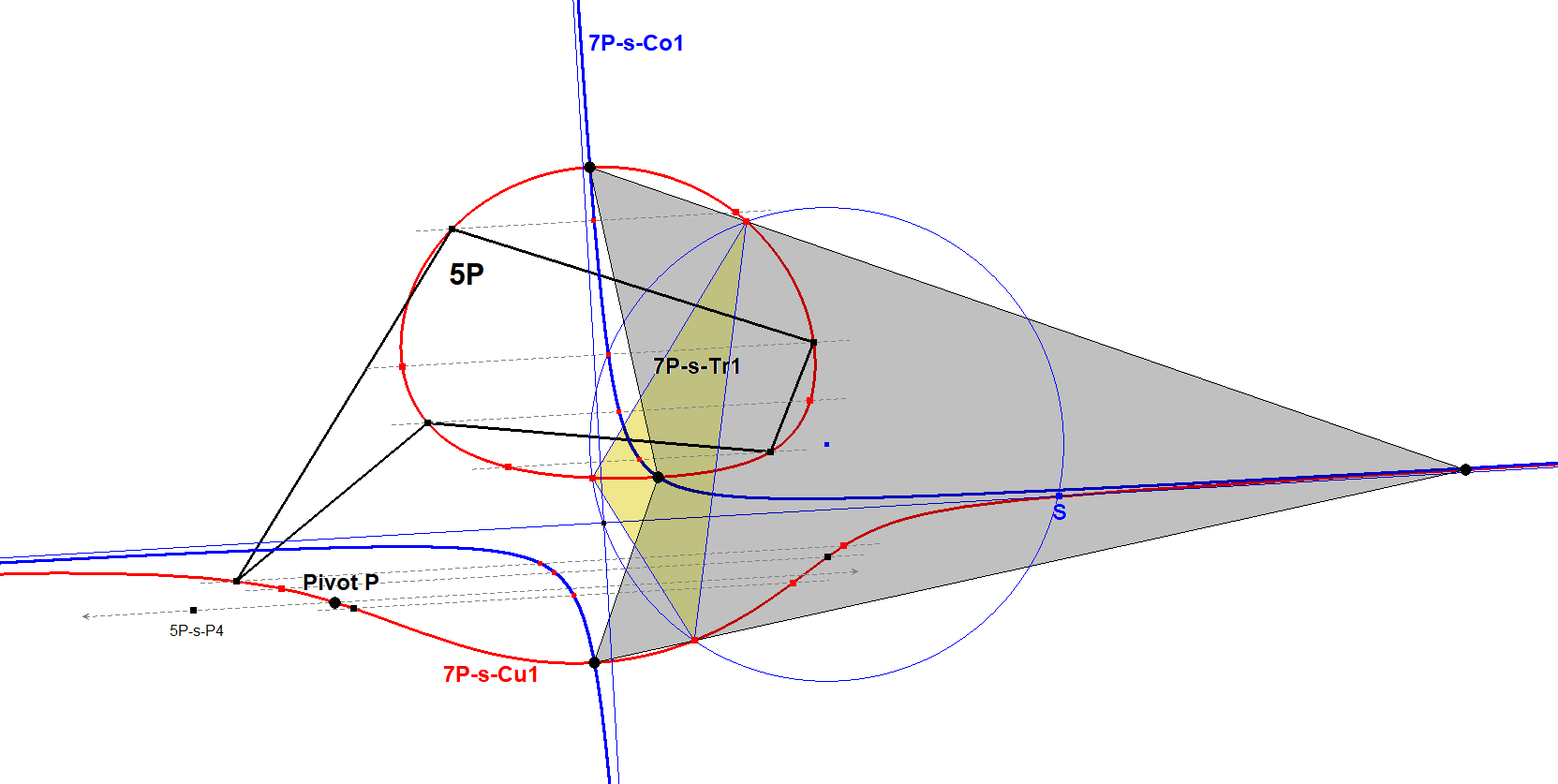
Properties
- one asymptote coincides with the asymptote of the cubic
- the hyperbola intersects the cubic in four points CUc2-4P, which are the in- and excenters of the CUc2-Tr1 Miquel Triangle. See QPG#1862.
- the hyperbola intersects the cubic in four points, the vertices of an orthocentric quadrangle (each vertex is orthocenter of the other three), whose diagonal triangle ABC is 7P-s-Tr1, and its circumcircle bears the center of 7P-s-Co1 and the intersection Q (7P-s-P5) of the cubic and its asymptote (7P-s-L1). See QPG#837.
Estimated human page views: 70
