CU-P-3P1

CU-P-3P1 The co-tangentials of P

On a general cubic CU we have 4 points of tangency (CU-P-4P1) of tangents from some point P to the cubic. They are the intersection points of CU and the P-Polar Conic (CU-P-Co1).

On the other hand, when one of these points of tangency is known, then the other three points of tangency can be constructed as follows:

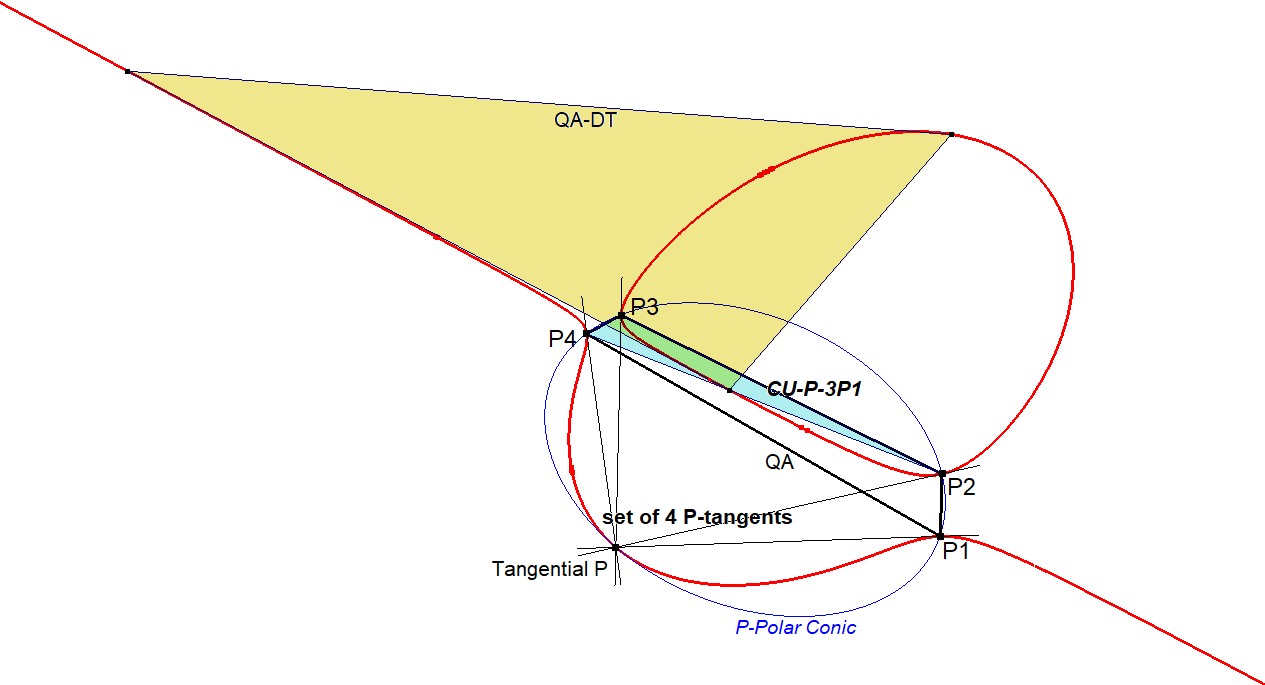
Construction 1

Let P1 be the known point on CU and let P2,P3,P4 be the other 3 CU-points that share the same tangential point P.
Since we only know P1 on the Cubic, we first construct its tangential P (see CU-P-P1).
Next, construct the P-Polar Conic (CU-P-Co1), which touches the cubic at each of the four points of tangency with respect to P. If the construction is done correctly, P1 will be among the four points intersection with CU.
The remaining 3 intersection points are the members of CU-P-3P1.
To avoid ambiguity caused by possible reordering of intersection points in dynamic geometry software, one may prefer to construct CU-P-3P as the AntiCevian Triangle of P1 wrt the Diagonal Triangle QA-DT of the Quadrangle (P1, P2, P3, P4).
To avoid ambiguity caused by possible reordering of intersection points in dynamic geometry software, one may prefer to construct CU-P-3P as the AntiCevian Triangle of P1 wrt the Diagonal Triangle QA-DT of the Quadrangle (P1, P2, P3, P4).

Infovisual CU-P-3P1-infovisual-cvt-01.jpg

CU-P-3P1 CU-points with same tangential – 01.fig

Construction 2

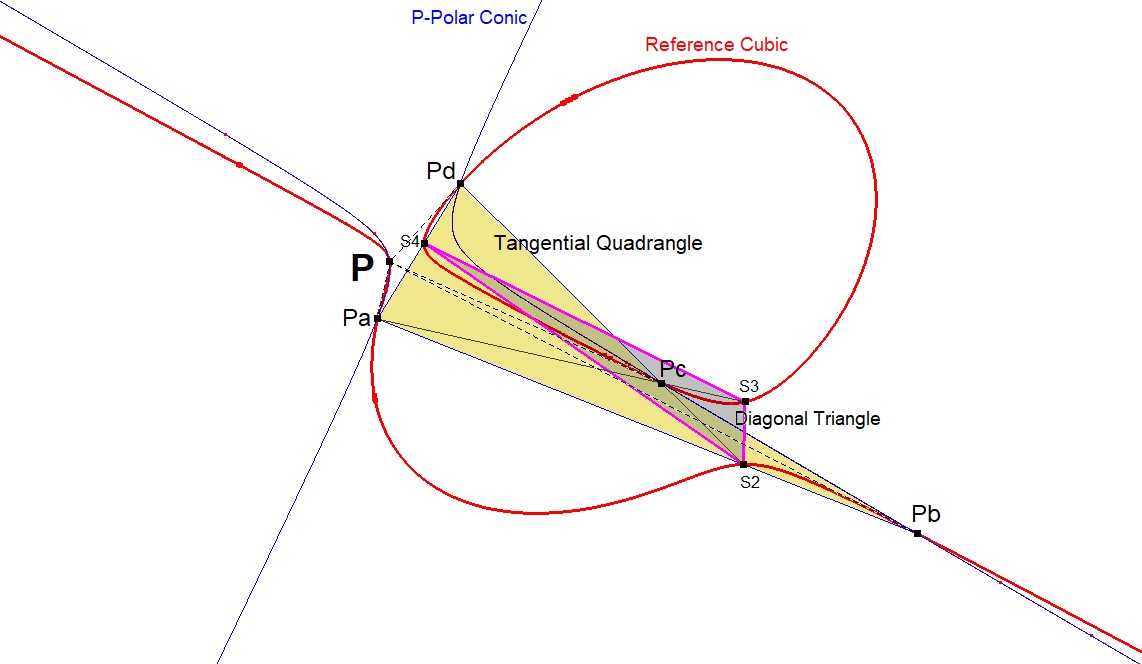
The next construction is based on the following property (see QPG#2722):

Let P be an arbitrary point on CU, and let (P1,P2,P3,P4) be the four points of tangency of the tangents from P to CU (also called tangentials).
Let (P1a,P1b,P1c,P1d) be the four tangentials of P1.
Now it turns out that the set (P2,P3,P4) coincides with the vertices (Q1a,Q1b,Q1c) of the Diagonal Triangle of the Quadrangle QA(P1a,P1b,P1c,P1d).

Therefore, the set CU-P-3P1 consists of the vertices of Diagonal Triangle of the Quadrangle formed by the four tangentials of P.

Infovisual CU-P-3P1-infovisual-cvt-02.jpg

CU-P-3P1 P-points with same tangential-01.fig

Note

Note that not for every cubic there will be 4 real intersection points of the P-Polar Conic CU-P-Co1. For example when CU is a monopartite cubic, then there will be 2 real intersection points and 2 imaginary intersection points. As a consequence, when P1 is a real point on a monopartite cubic CU, then CU-P-3P1 will consist of 1 real point and 2 imaginary points.

Estimated human page views: 6