nL-n-iL1: nL-Morley’s Axes
Morley describes in his document Ref-37 , page 470 that in an n-Line nn-1 Axes can be constructed mutually crossing at angles of i.π/n. Moreover the angles of these axes with some random line will be the mean angle of the angles of L1,L2, … ,Ln with that random line eventually corrected with i.π/n.
So in a Triangle (3-Line) there are 3×3 axes mutually crossing at i.600. These are the sides of the well-known equilateral Morley Triangle complemented with 6 other parallel axes.
In a Quadrilateral (4-Line) there are 4x4x4 axes mutually crossing at i.450. These 64 axes are hardly known and there is no literature known about its construction.
In the Yahoo Quadri-Figures Group ([34]) there was a discussion in the period October 2014-April 2015 on this subject by Bernard Keizer (France), Eckart Schmidt (Germany) and Chris van Tienhoven (Netherlands). Finally Bernard Keizer found a solution for the construction of these axes in a 4-Line. See [34], QFG#1032. The general method for n-Lines was described by Chris van Tienhoven. See [34], QFG#1138.
Construction
The Lighthouse Theorem is needed for constructing the nL-Morley Axes.
The Lighthouse Theorem was discovered by R. K. Guy of the University of Calgary (Ref-57).The Lighthouse Theorem describes how regular polygons can be constructed from the intersection points of regular beams emanating from two Lighthouses.
For constructing the nL-Morley Axes an extended version of the Lighthouse Theorem is introduced of n collinear Lighthouses also producing (semi-)regular polygons. The Lighthouse Theorem for two Lighthouses can be used for constructing Morley’s Trisector Theorem in a triangle. The extended Lighthouse Theorem is useful for constructing Morley’s Axes in an n-Line.
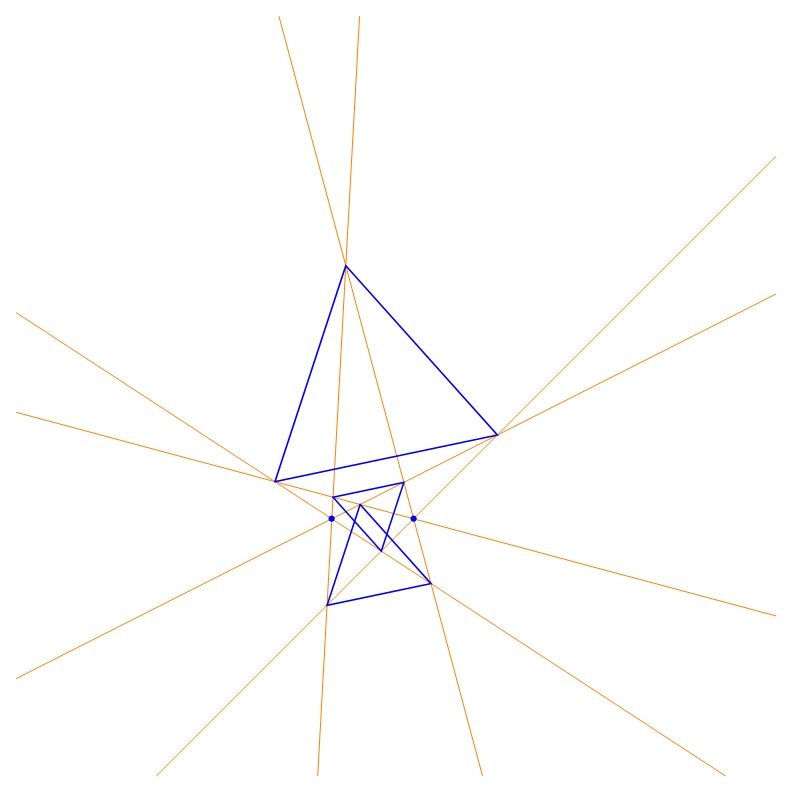
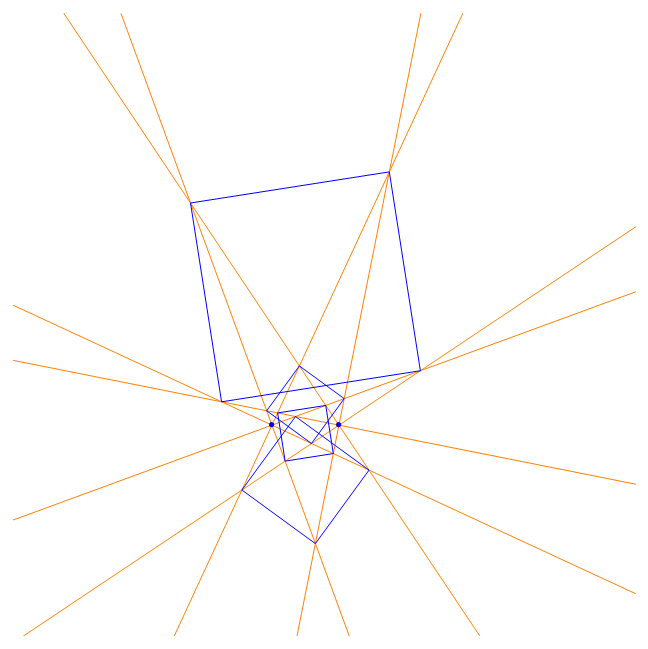
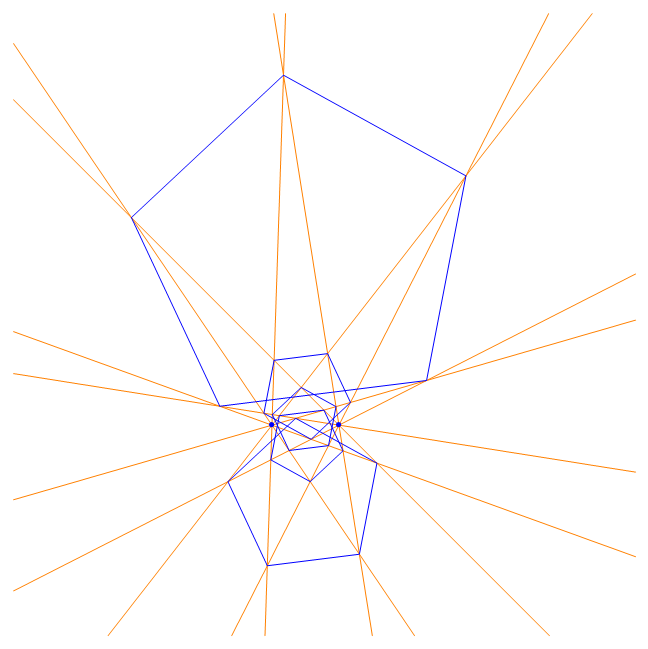
According to the regular Lighthouse Theorem there should be known two points (Lighthouses) and two initial lines (beams) emanating from these points and a number n describing the angle π/n with which the beams n times will be rotated (n is a natural number). The result is n regular n-gons.
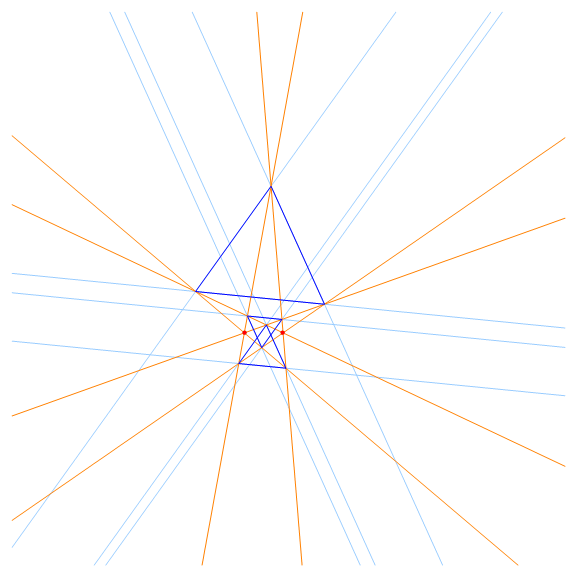
According to the extended Lighthouse Theorem when are known m collinear points (Lighthouses) with a set of accompanying initial beams and a number n describing the angle π/n used for rotating the beams n times (m and n are natural numbers) then nm-1 semi-regular n-gons (sides crossing at angles i.π/n) can be constructed from intersection points at consecutive levels from these beams. For explanation and details see [34], QFG #1138.
Any nL-Morley Axis (being a side of the semi-regular n-gons) is uniquely defined by a constellation of (n-1) Lighthouses with a set of accompanying initial beams and a rotation-angle π/n.
Examples regular Lighthouse Theorem
 |
 |
 |
|
2 Lighthouses each emanating 3 beams produce 3 regular 3-gons |
2 Lighthouses each emanating 4 beams produce 4 regular 4-gons |
2 Lighthouses each emanating 5 beams produce 5 regular 5-gons |
Examples Extended Lighthouse Theorem
 |
 |
 |
|
2 Lighthouses each emanating 3 beams produce 31 regular 3-gons (i=0,1,2) giving 32=9 axes at angles i.600 (i=0,1,2) |
3 Lighthouses each emanating 4 beams produce 42 semi-regular 4-gons giving 43=64 axes at angles i.450 (i=0,1,2,3) |
4 Lighthouses each emanating 5 beams produce 53 semi-regular 5-gons (1 shown) giving 54=625 axes at angles i.360 (i=0,1,2,3,4) |
Relationship with n-Lines
- In an n-Line there are n random lines. One of these lines (say L0) can be chosen as baseline. The other (n-1) lines cross this baseline in just as many intersection points P1, P2, … , Pn-1 (it will appear that changing the baseline will give the same results).
- These (n-1) intersection points can be considered as (n-1) collinear Lighthouses.
- Let a1, a2, …, an-1 be the directed angles between baseline L0 and lines L1, L2, … , Ln-1. The directed angle between L0 and Li is defined as the angle needed for rotating L0 anti-clockwise onto Li.
- Rotating L0 in P1, P2, … , Pn-1 resp. about angles a1/n, a2/n, …, an-1/n will produce the n-sectors of the defining lines L1, L2, … , Ln-1 with L0 nearest to L0.
- By rotating these n-sectors (n-1) times about rotation-angle π/n we end up with the n beams emanated from (n-1) Lighthouses.
- Now we have (n-1) collinear Lighthouses each emanating n beams.
- Per Lighthouse we can choose one beam from these n beams per Lighthouse. Together they are the initial beams emanated from (n-1) Lighthouses defining a unique nL-Morley Axis. For details see [34], QFG#1138.
- Since per Lighthouse of the (n-1) Lighthouses there are n beams to be chosen as initial beam we finally have nn-1 Morley Axes.
Properties
- In an n-Line the n times (n-1)n-2 Morley axes of the component (n-1)-Lines meet in (n-1)n-1 incenters, there being n axes on a point and (n-1) points on an axis. See Ref-37, page 470. These incenters are the centers of the EnnaCardioids nL-n-Cv1.
Estimated human page views: 339
