← Previous Next →

nL-n-P6: nL-Least Squared Distances Point

nL-n-P6 is the unique point in an n-Line with the Least Sum of Squared Distances to its n Lines.

nL-n-P6 can be constructed in a recursive way:

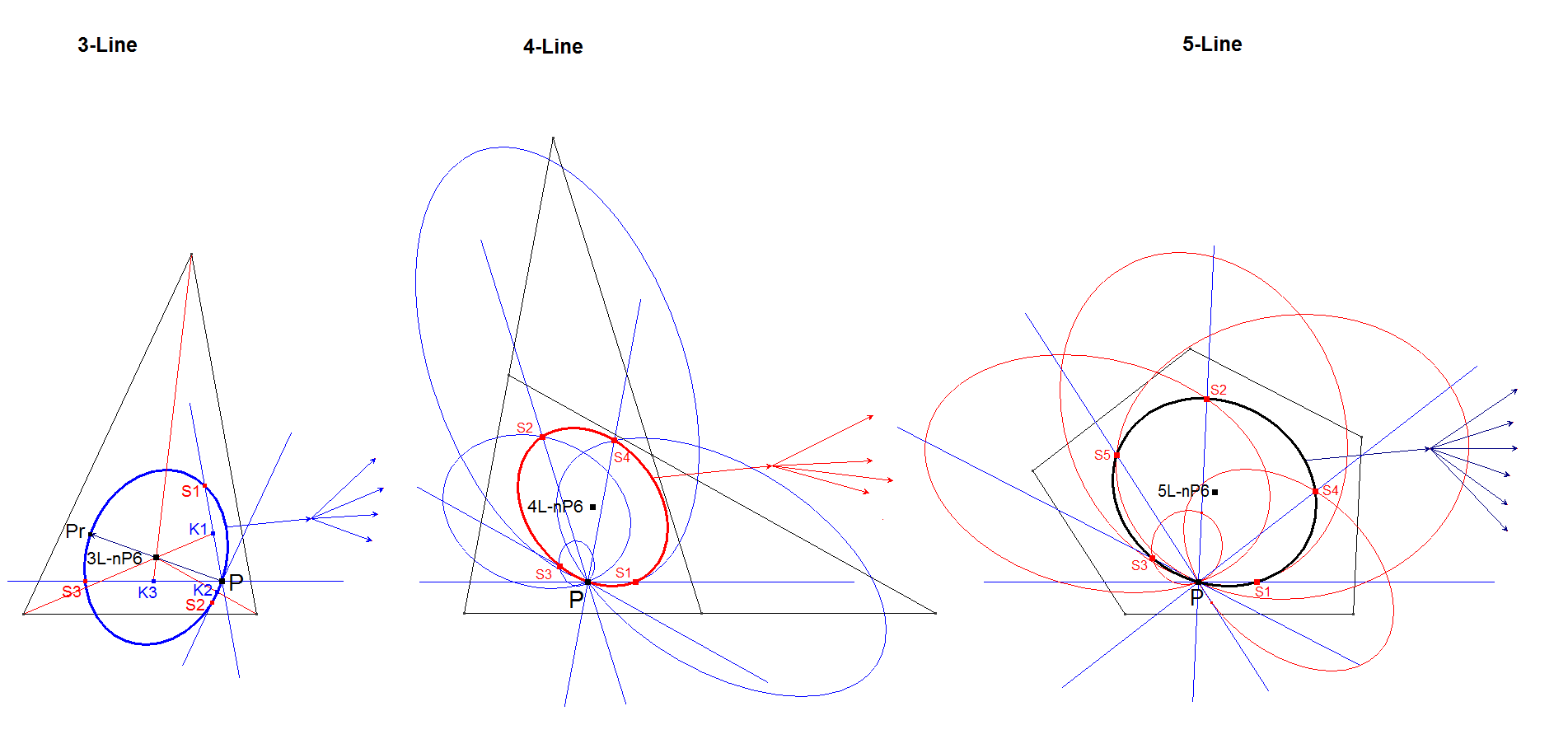
Infovisual nL-n-P6-infovisual-cvt-01.png

The nL-n-P6 point can be constructed because in an n-Line the points with an equal sum of squared distances lie on an ellipse. See [34], QFG #1617, #1622.

This ellipse with a Fixed Sum of Squared Distances is called here an FSD-ellipse and when passing through P it is called the P-FSD-ellipse. The point with Least Sum of Squared Distances is the center of any FSD-ellipse.

A P-FSD-ellipse can be constructed by drawing lines in an n-Line through P parallel to the n Lines. Now on each of these parallel lines there will be a second point next to P with the same fixed sum of squared distances also lying on the P-FSD-ellipse. When we find 5 of these second points we have defined a conic and this conic should be the P-FSD-ellipse. Actually 4 points will be enough for construction because P is per definition also on the conic.

Per level a P-FSD-ellipse is constructed that will be transferred to the next level. The center of the P-FSD-ellipse is nL-n-P6 for that level.

Construction in a 3-Line (triangle)

This is the lowest level which differs from the general case.

  1. Let P be some arbitrary point and K be the Symmedian Point X(6) in a triangle. X(6) is the nL-Least Squares Point of a triangle.
  2. Draw lines Lp1,Lp2,Lp3 through P parallel to the sidelines L1,L2,L3,
  3. Let K1,K2,K3 be the intersection points of Lp1,Lp2,Lp3 and the resp. symmedians through the triangle vertices L2^L3, L3^L1, L1^L2.
  4. Let S1,S2,S3 be the reflections of P in K1,K2,K3.
  5. Let Pr be the reflection of P in K.
  6. The conic through P, Pr, S1, S2, S3 will be the P-FSD-ellipse.

In a similar way we can construct a P-FSD-ellipse in a 4-Line (quadrilateral).

  1. Let L1,L2,L3,L4 be the 4 defining lines of the 4-Line.
  2. Draw lines Lp1,Lp2,Lp3,Lp4 through arbitrary point P parallel to the sidelines L1,L2,L3,L4.
  3. We are searching for the second point on Lp1 with same sum of squared distances to L1,L2,L3,L4 as P has. When we vary P on Lp1 at least the distance to L1 is fixed. So we have to find the point with fixed sum of squared distances to L2,L3,L4. This is the FSD-triangle problem like described here before. So construct the P-FSD-ellipse wrt triangle L2.L3.L4. Let S1 be the 2nd intersection point of this P-FSD-ellipse with Lp1. S1 has the same fixed sum of squared distances to L1,L2,L3,L4 as P.
  4. Accordingly we can construct S2, S3, S4.
  5. The conic through P, S1, S2, S3, S4 will be the P-FSD-ellipse in a 4-Line (quadrilateral).
  6. The center of this ellipse is QL-P26 indeed. See EQF.

In a similar way we can construct a P-FSD-ellipse in a 5-Line (pentalateral).

  1. Let L1,L2,L3,L4,L5 be the 5 defining lines of the 5-Line (pentalateral).
  2. Draw lines Lp1,Lp2,Lp3,Lp4,Lp5 through arbitrary point P parallel to the sidelines L1,L2,L3,L4,L5.
  3. We are searching for the second point on Lp1 with same sum of squared distances to L1,L2,L3,L4,L5 as P has. When we vary P on Lp1 at least the distance to L1 is fixed. So we have to find the point with fixed sum of squared distances to L2,L3,L4,L5. This is the FSD-triangle-problem for a 4-Line like described here before. So construct the P-FSD-ellipse wrt quadrilateral L2.L3.L4.L5. Let S1 be the 2nd intersection point of this P-FSD-ellipse with Lp1. S1 has the same fixed sum of squared distances to L1,L2,L3,L4,L5 as P.
  4. Accordingly we can construct S2, S3, S4, S5.
  5. The conic through P, S1, S2, S3, S4 will be the P-FSD-ellipse in a 4-Line (quadrilateral). It will appear that S5 is also on the conic.
  6. The center of this ellipse will be the LSD-point of a 5-Line.

In a recursive way P-FSD-ellipses can be constructed in every n-Line (n>2) and the center of this P-FSD-ellipse will be the LSD-points of the n-Line.

Another Construction

Coolidge describes in Ref-25 a general method for constructing this point in an n-Line.

In this picture an example is given in a 4-Line, where nL-n-P6 = QL-P26.

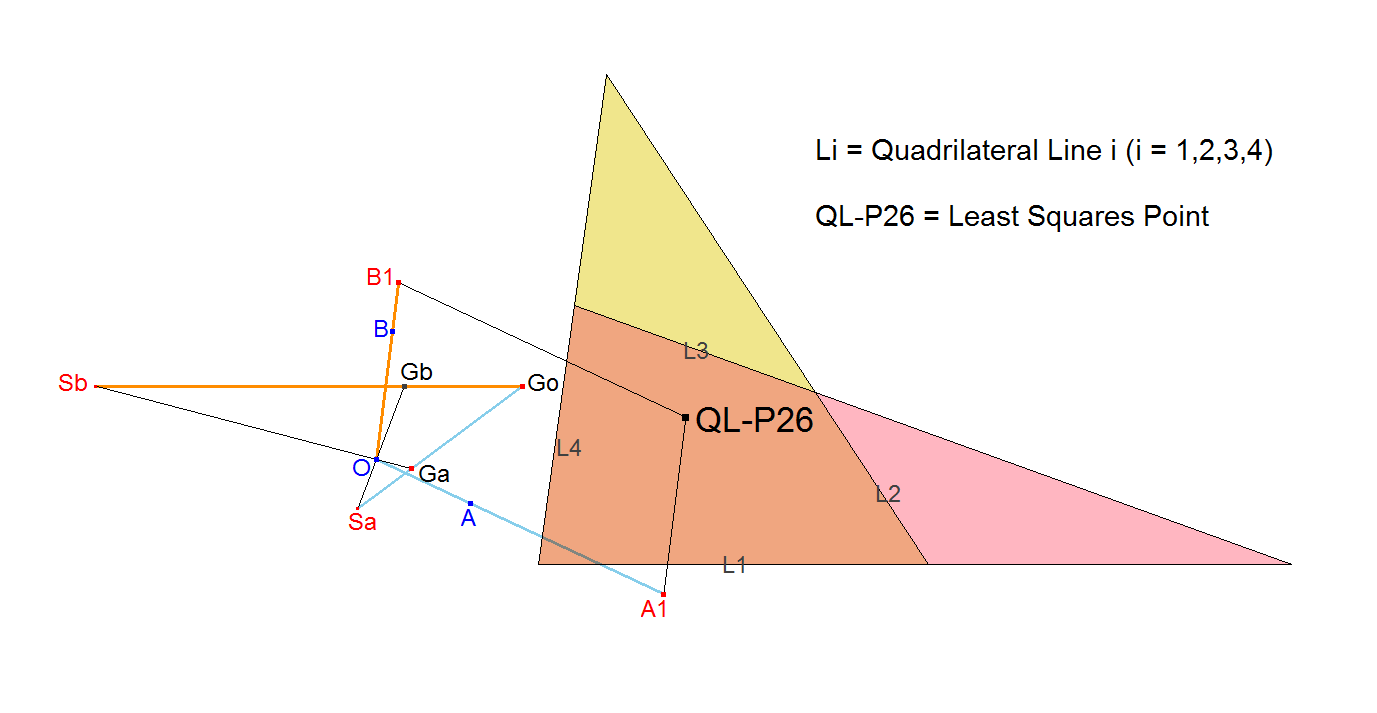
Infovisual nL-n-P6-infovisual-cvt-02.png

This construction is a modified version of the construction of Coolidge.

  • Let O (origin), A and B be random non-collinear points.
  • Go = Quadrangle Centroid of the projection points of O on the n basic lines of the Reference n-Line.
  • Ga = Quadrangle Centroid of the projection points of O on the n lines through point A parallel to the n basic lines of the Reference Quadrilateral.
  • Gb = Quadrangle Centroid of the projection points of O on the n lines through point B parallel to the n basic lines of the Reference Quadrilateral.
  • Let Sa = Ga.Go ^ O.Gb and Sb = Gb.Go ^ O.Ga.
  • Construct A1 on line O.A such that Sa.Ga : Ga.Go = O.A : A.A1.
  • Construct B1 on line O.B such that Sb.Gb : Gb.Go = O.B : B.B1.
  • Construct P such that O.A1.P.B1 is a parallelogram and where O and P are opposite vertices. P is the Least Squares Point nL-n-P6.
Correspondence with ETC/EQF
  • When n=3, then nL-n-P6 = X(6).
  • When n=4, then nL-n-P6 = QL-P26.


Estimated human page views: 300

Scroll naar boven