6P-s-Tf1 6P-Schmidt Transformation
Let 6P be the Reference 6-Point (Hexangle) and P a random Point.
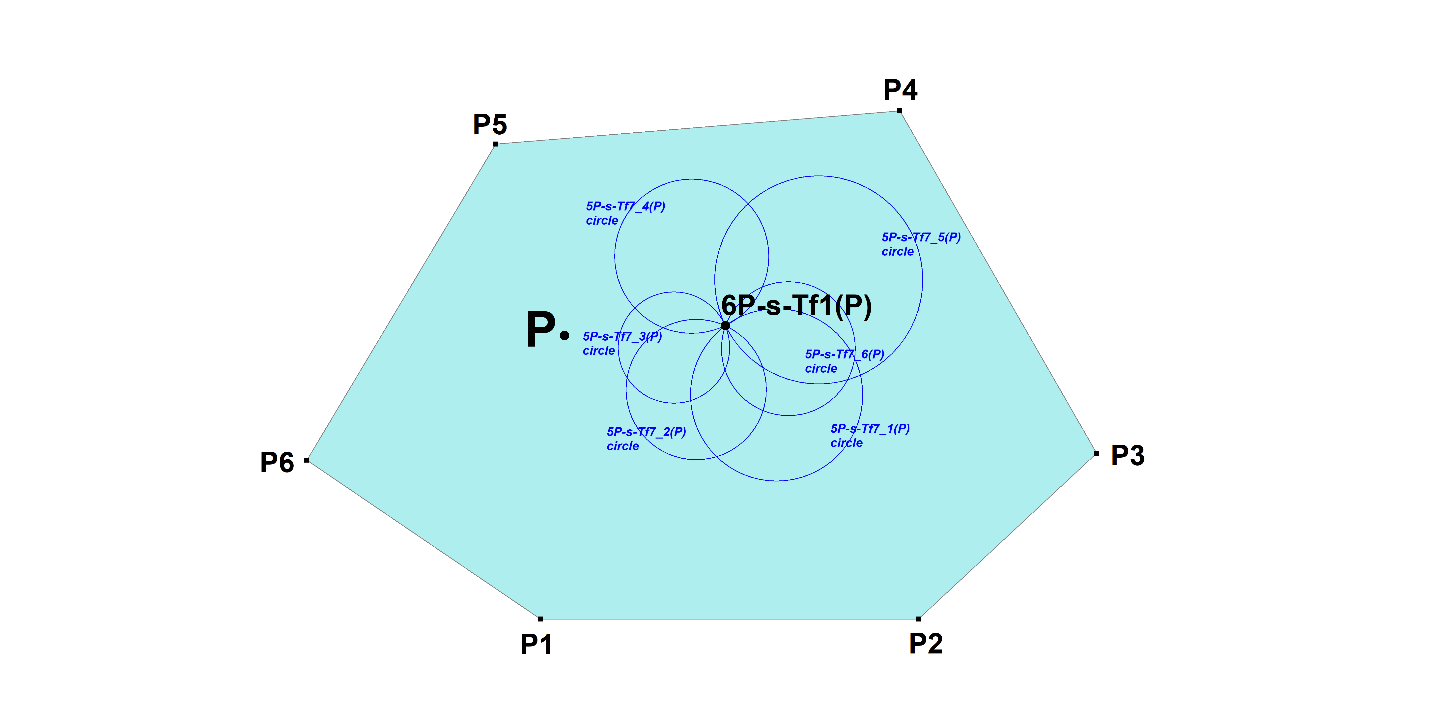
The Reference 6-Point has six component 5-Points (Pentangles).
The 5P-s-Tf7-circles of these six component 5-Points concur in one point 6P-s-Tf1(P).
This transformation was found by Eckart Schmidt. See [34], QFG-message #3575.
Properties
- 6P-s-Tf1(P) lies on 6P-s-Ci1.
- All points in the plane mapped by 6P-s-Tf1 lie on 6P-s-Ci1. Exceptions are the 6P-vertices and points lying on lines Pi.Pj, their images are indetermined. See [66], QPG-message #653, #654 and #657.
- When we consider a circular cubic Cux = 7P-s-Cu1(P1,P2,P3,P4,P5,P6,Px), where Px is some point on 6P-s-Ci1, then 6P-s-Tf1(X) = 6P-s-Tf1(Px) for all points X on Cux. Hence we have a pencil of circular cubics, all passing through 6P-s-P2 and each corresponding with its own unique point on circle 6P-s-Ci1. See [66], QPG-message#653 and #657.
Estimated human page views: 242
