PR-1 Notes on Perspective Scales
Structural definition of a Perspective Scale
A perspective scale is an ordered linear configuration consisting of a sequence of collinear points (P1, P2, P3, . . . ).
together with a distinguished point V on the same line, called the vanishing point.
The points (Pi) are successive points as they appear under a given perspectival projection, and the pair ({Pi}, V) determines the perspectival setting on that line.
Constructive definition of a Perspective Scale and its Norm
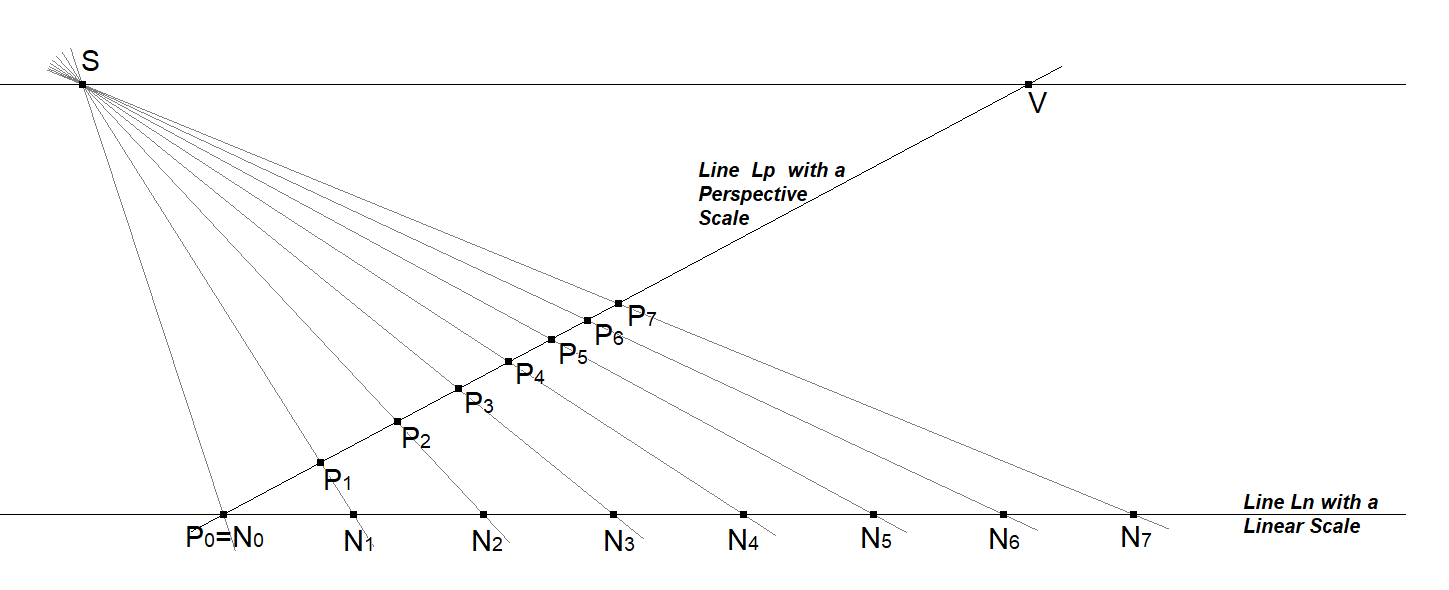
Let \(L_n\) be a line equipped with a linear scale of equally spaced points \(N_0, N_1, N_2, N_3, \dots\).
Let \(L_p\) be a second line through \(N_0\).
Choose two successive points \(P_1\) and \(P_2\) on \(L_p\) , and set \(P_0 := N_0\) .
Define \(S = (N_1P_1) \cap (N_2P_2)\).
Let \(V\) be the intersection of \(L_p\) with the line through \(S\) parallel to \(L_n\).
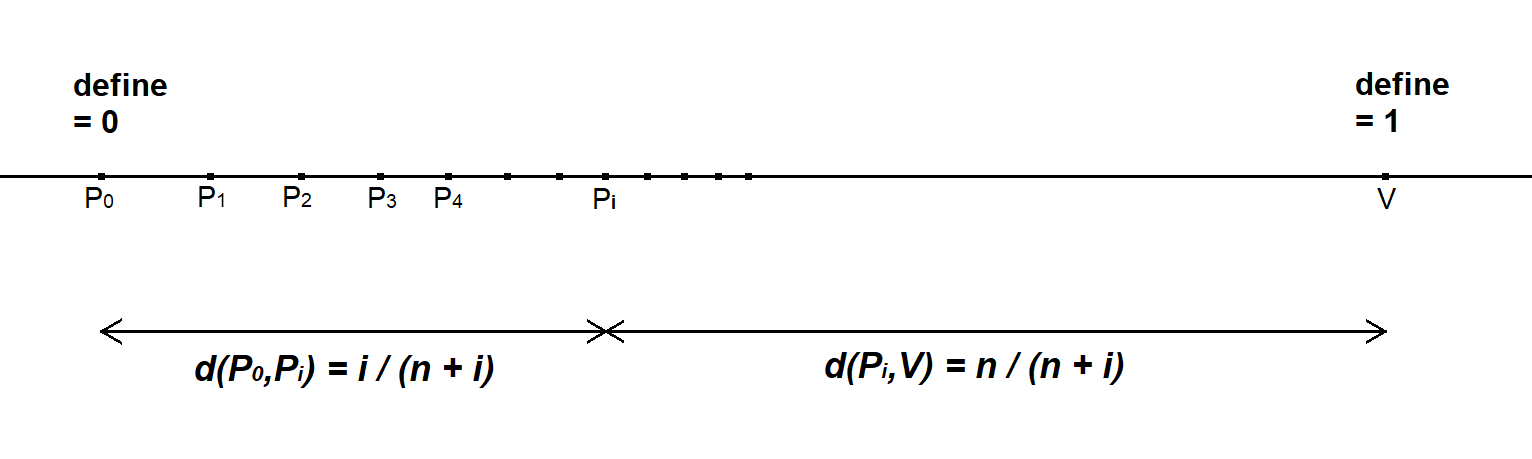
This construction is purely projective. Normalize the distance \(d(P_0, V) = 1\).
Under this normalization, the points \(P_i\) constructed analogously on \(L_p\) satisfy \[ d(P_0, P_i) = \frac{i}{n+i}, \qquad i = 1,2,3,\dots, \] for a unique positive real parameter \(n\).
This parameter \(n\) is called the perspective norm of the scale and can be recovered from \[ d(P_0, P_1) = \frac{1}{n+1}. \]
All Perspective Scales with the same perspective norm \(n\) are projectively equivalent once normalized by \(d(P_0, V) = 1\). Thus different Perspective Scales are distinguished solely by their perspective norm.
Estimated human page views: 149
